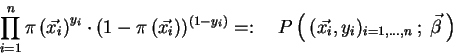``Logistic regression'', like Fisher's Method and the Perceptron (Section 3.1.1) is a supervised method for the two class classification problem [16]. Though a different model is used, it can be shown that logistic discrimination and Fisher discrimination are the same when sampling from multivariate distributions with common covariance matrices [17].
Logistic regression tries to model the (logarithmic) odds-ratio
for the classification (variable Y) as a linear function of the
p ``input'' variables
![]() ;
;
![]() is the (p+1) dimensional coefficient vector:
is the (p+1) dimensional coefficient vector:
The odds-ratio is the factor of how many times the event (Y=1) is more
likely to happen than event (Y=0) given the knowledge of X.
By taking the logarithm we map the values
![]() to
to
![]() .
As:
.
As:
![\begin{displaymath}f( Y=1 \vert \vec{X}) > f( Y=0 \vert \vec{X}) \quad \Leftrigh...
...frac{f( Y=1 \vert \vec{X})}{f( Y=0 \vert \vec{X})} \right] > 0 \end{displaymath}](img98.gif)
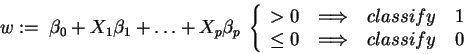
which is the same (n-1) dimensional hyperplane as used by the linear classifiers. Actually we can use all different kinds of functions to model the logarithmic odds ratio. We could also weight our classification in such a way that we only classify something as ``1'' if the probability for this event is higher then some given probability p. This just means changing 0 to a different value in the above formula.
In standard logistic regression the model-parameters ![]() are obtained
via maximum likelihood estimators. By transforming the model 15 for the
log-odds-ratio we get
are obtained
via maximum likelihood estimators. By transforming the model 15 for the
log-odds-ratio we get
![]() :
:
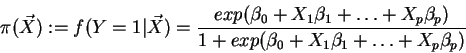 |
(16) |