Fisher / Perceptron (NN) - linear classifiers

Fisher's method [10], [20, pp. 470] is a supervised method for the classification-problem into two classes by using the knowledge of some continuous input-variables. It corresponds to the historic Neural Network ``Perceptron'' [37] (also known as ``Linear Machine'') but uses a different approach for ``learning'' the model.

Let $\vec{X}=[X_1,X_2,\ldots , X_p]$ be the known continuous p input-variables, and Y the classification variable with two states. Fisher's method assumes that the conditional Probability distributions are normally distributed with the same (invertible) covariance matrix:

$$f( \vec{X} \vert Y=0) \sim N(\vec{\mu_0}, \Sigma),\qquad E( \vec{X} \vert Y=0) = \vec{\mu_0}$$

$$f( \vec{X} \vert Y=1) \sim N(\vec{\mu_1}, \Sigma),\qquad E( \vec{X} \vert Y=1) = \vec{\mu_1}$$

The normal distribution assumption guaranties optimal fit of the model, but is not necessary, whereas the assumption of same covariance matrices can be critical for Fisher's model calculation.

Now the aim of the method is to find a linear combination of the variables X_i which is best able to discriminate the two classes of Y. Formally, we are are looking for a vector l:

$$W=l^T \cdot \vec{X}$$

such that:

$$\frac{(E(W \vert Y=1) - E((W \vert Y=0))^2}{VAR(W)}$$

is maximal.

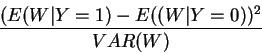
This vector l defines the best linear combination of the X_i variables for the scalar (univariate) random variable W to discriminate between the two classes (the difference between the conditional expected values are maximal with respect to its variance). The expected values and variance are:

$$\bar{w_0} := E( W \vert Y=0) = l^T \vec{\mu_0}$$

$$\bar{w_1} := E( W \vert Y=1) = l^T \vec{\mu_1}$$

$$VAR(W) = l^T \Sigma l$$

For classifying a new observation $\vec{x}^* \in dom(\vec{X})$ we just multiply it with lto calculate its linear combination (the value of the random variable W). Then we classify according to this value. If it's closer to the mean $\bar{w_0}$ then we classify it as class 0, otherwise as class 1. Let $m := \frac{\bar{w}_0+\bar{w}_1}{2}$, and assume $\bar{w}_1 > \bar{w}_0$, then the classificiation for x^* is:

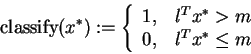$$\mbox{classify}(x^*) := \left\{ \begin{array}{r@{,\quad}l} 1 & l^T x^* > m \\ 0 & l^T x^* \le m \end{array}\right.$$ (13)

The remaining question is how to train the model, how to obtain the vector l. Here Fisher's Method and the Perceptron differ in their approaches.

If both populations $f(\vec{X}\vert Y=0)$ and $f(\vec{X}\vert Y=1)$ have the same covariance-matrix $\Sigma$, then:

$$l^T = (\vec{\mu_1} - \vec{\mu_0})' \Sigma^{-1}$$ (14)

maximizes the differences of the expected values relative to the variance of W. From the generalized Cauchy-Schwarz inequality:

$$(l^T \delta)^2 \le (l^T \Sigma l)(\delta^T \Sigma \delta)$$

it follows (letting $\delta := \vec{\mu_1} - \vec{\mu_0}$ ):

$$\frac{(E(W \vert Y=1) - E((W \vert Y=0))^2}{VAR(W)} = \frac... ...^T \delta)^2}{ l^T \Sigma l} \le \delta^T \Sigma^{-1} \delta$$

Substituting $l^T = (\vec{\mu_1} - \vec{\mu_0})^T \Sigma^{-1}$ we reach this maximum:

$$\frac{(l^T \delta)^2}{ l^T \Sigma l} = \frac{ ((\vec{\mu_1}... ...\Sigma^{-1} \Sigma \Sigma^{T\:-1} (\vec{\mu_1} - \vec{\mu_0})}$$

$$= \frac{ (\delta^T \Sigma^{-1} \delta)^2} { \delta^T \Sigma^{-1} \delta}$$

$$= \delta^T \Sigma^{-1} \delta$$

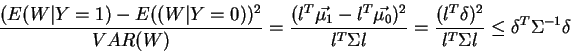
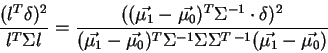
Fisher's Method uses this result to derive the statistically ``optimal'' model. The Covariance-matrix $\Sigma$ and the means $\vec{\mu_0}$ and $\vec{\mu_1}$ are obtained via unbiased estimators [20, pp. 474]. In this case the random variable W is also known as ``Fisher's Sample Linear Discrimination Function''.

While Fisher's Method is grounded on statistical inference the Perceptron doesn't make any assumptions about the distributions. The Perceptron with initial random weights (the vector l) is sequentially given training data for classification. Whenever the classification is wrong l is adjusted by adding or subtracting (depending on the right classification) a learning-parameter $\lambda$times the input vector. It is known that the ``weight-vector'' l of the Perceptron will converge [37].

How do these methods relate to the presented basic structure-finding techniques? First of all they require continuous variables and don't work with nominal data. But as they are famous historical methods I wanted to present them for completeness and for understanding of the structure-finding problem. They also state good examples for using the technique of creating new dimensions.

In this case the new dimension is computed by a linear combination of the other dimensions. The aim is to select this dimension according to the model such that the conditional distributions $f(\vec{X}\vert Y=0)$ and $f(\vec{X}\vert Y=1)$ are as different as possible. Using these linear methods means that we are looking for an n-1 dimensional hyperplane in the n-dimensional variable-space for separating our 2 classes; we are looking for one new dimension which then can be used projected and conditionalized for classifying new unknown data entities.