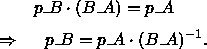Die Transformation von einem Koordinatensystem in ein anderes bedeutet
einen Basiswechsel und läßt sich
folgendermaßen formalisieren:
Gegeben sei ein Koordinatensystem A , in dem ein anderes
Koordinatensystem B durch die homogenen Koordinaten des Ursprungs
( Bw ) und die drei normierten Richtungsvektoren der Achsen ( Bx , By , Bz )
definiert ist.
Zeilenweise angeordnet ergeben diese Vektoren die Matrix
B _ A , die den Übergang vom Koordinatensystem B zum
Koordinatensystem A beschreibt:
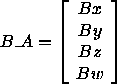
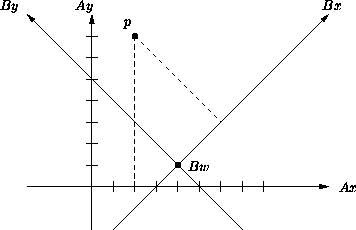
Beispiel (für den 2-dimensionalen Fall):
| x -Achse: | Bx | lautet |
[ ,,0] |
| y -Achse: | By | lautet |
[- ,,0] |
| Ursprung: | Bw | lautet | [4,1,1] |
| Punkt: | p _ B | lautet |
[2 ·  ,4 · ,1] |
Der Aufbau der Matrix B
repräsentiert die erforderliche Drehung und
Verschiebung, um einen aus der Sicht
von Koordinatensystem
B beschriebenen Punkt p aus der Sicht von Koordinatensystem A zu
beschreiben. Im zwei-dimensionalen Fall wird
zunächst der Punkt p um den Winkel 
gedreht,
der sich zwischen den Achsen der Koordinatensysteme A und B befindet. Dann
wird eine Translation durchgeführt mit dem Wert der Ursprungsposition
von B . Cosinus und Sinus des Drehwinkels ergeben sich
gerade aus den Werten a bzw. b , wobei die
Einheitsvektoren (a,b) und (- b,a)
die Basis für Koordinatensystem B darstellen.
Also läßt sich in obigem Beispiel der Punkt p wie folgt transformieren:
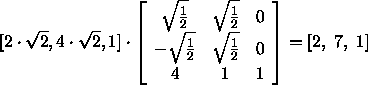
Um einen Punkt p _ A
des Koordinatensystems A im Koordinatensystem B
zu spezifizieren, verwendet man die inverse
Matrix zu B _ A :
