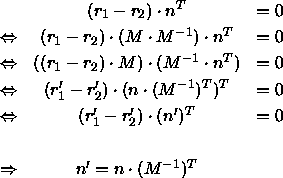Die Normalenvektoren müssen bei der Transformation von Objektpunkten ebenfalls
abgebildet werden.
Allgemein gilt,
daß bei der Transformation eines Objekts mit der Matrix M ein Normalenvektor n
dieses Objekts mit der transponierten Inversen von M abgebildet
werden muß:
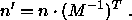
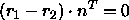
Bei einem Wechsel des Koordinatensystems
werden die Ortsvektoren r1 und r2 mit
der Matrix M transformiert:
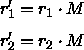
Es gilt: