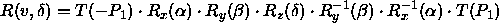13.3 Rotation

Rotation um die z -Achse

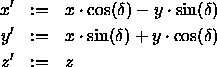
Die daraus resultierende Transformationsmatrix lautet:

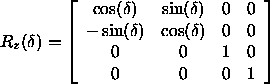
Rotation um die x -Achse

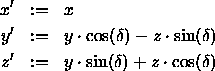
Die daraus resultierende Transformationsmatrix lautet:

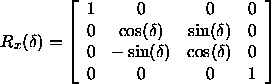
Rotation um die y -Achse

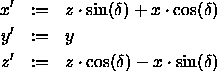
Die daraus resultierende Transformationsmatrix lautet:

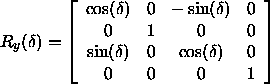
Rotation um eine beliebige Achse

Voraussetzung: Die Rotationsachse stimme nicht mit einer der Koordinatenachsen überein.

Idee:

Transformiere Rotationsachse und Objekt so, daß die Rotationsachse mit der z -Achse übereinstimmt, rotiere um vorgegebenen Winkel , transformiere zurück.

1.

Translation von Rotationsachse (und Objekt), so daß die Rotationsachse durch den Ursprung läuft.

2.

Rotation der Rotationsachse um die x -Achse in die xz -Ebene.

3.

Rotation der Rotationsachse um die y -Achse in die z -Achse.

4.

Rotation des Objekts um die z -Achse mit Winkel .

5.

Rücktransformation des gedrehten Objekts durch Anwendung der inversen Transformationen der Schritte (3), (2) und (1).

Ist die Rotationsachse durch die Punkte P₁,P₂ gegeben, so gilt

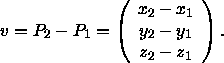
Die Länge dieses Vektors lautet

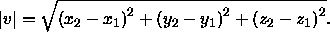
Die Komponenten des zugehörigen Einheitsvektors

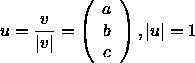
lauten daher

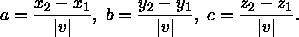
Schritt 1 läßt sich durch die Translation T(- x₁, - y₁, - z₁) durchführen. Dadurch wird P₁ , Ausgangspunkt des Einheitsvektors u , in den Ursprung verschoben.

Für Schritt 2 sind Sinus und Cosinus des Rotationswinkels erforderlich, der zwischen der Projektion u' von u auf die yz -Fläche und der z -Achse, repräsentiert durch den Vektor u_z = (0,0,1) , liegt.

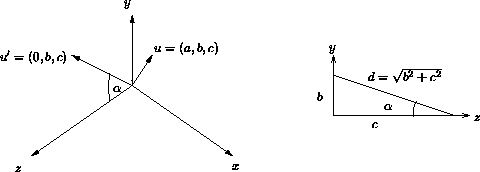
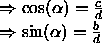
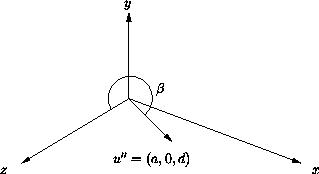
Nach Schritt 2 befindet sich der ursprüngliche Vektor u als u'' in der xz -Ebene:

Für Schritt 3 (Rotation um y -Achse) benötigt man Sinus und Cosinus des Rotationswinkels .

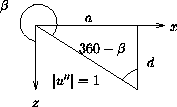
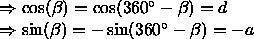
Nach den ersten drei Schritten ist die Drehachse mit der z -Achse identisch, so daß Schritt (4) mit der Rotationsmatrix R_z() durchgeführt werden kann. Schritt (5) beinhaltet die Anwendung der inversen Transformationen.

Die Rotation um die Achse v = um den Winkel läßt sich daher wie folgt darstellen: