



| Gegeben: |
Ungerichteter, ungewichteter Graph G = (V,E) |
| Gesucht: |
Zusammenhangskomponenten, d.h. zhk[i] = j, falls Knoten i sich in der j -ten
Zusammenhangskomponente befindet. |
huell[i,j]= 1
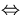 es gibt Weg von i nach j .
es gibt Weg von i nach j .
Sei A die (boole'sche) Adjazenzmatrix.
Dann bilde
A j = A j - 1 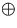 A
A 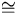 Wege der Länge j .
Wege der Länge j .
Läßt sich abkürzen durch
A,A 2,A 4,A 8,....
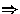 log n boole'sche Matrixmultiplikationen
log n boole'sche Matrixmultiplikationen
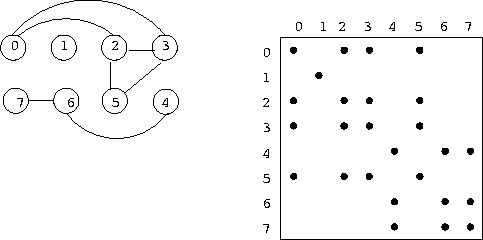
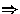 log n Schritte für eine CRCW-PRAM mit
n 3 Prozessoren.
log n Schritte für eine CRCW-PRAM mit
n 3 Prozessoren.
Graph und seine transitive Hülle
Liegt der erste Eintrag von Zeile i in Spalte j ,
so gilt zhk[i] = j.
Kosten:
O(n 3 · log n) .
Partitioniere die Adjazenzmatrix in p Streifen.
Jeder Prozessor berechnet einen Spannwald durch Tiefensuche.
Anschließend werden die Spannwälder mit UNION-FIND
ineinandergemischt.
Dazu wird jede Kante (x,y) vom sendenden Prozessor
beim empfangenden Prozessor daraufhin getestet, ob x
und y in derselben ZHK liegen.
Falls ja, wird (x,y) ignoriert, falls nein, werden ZHK(x) und
ZHK(y) verbunden.
Da jeder Wald höchstens n Kanten
enthält, benötigt das Mischen O(n) .
Im Hypercube mit p Prozessoren entstehen nach der initialen Tiefensuche
mit Zeit
O(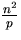 ) anschließend log p Mischphasen der Zeit
O(n) .
Also beträgt die Gesamtzeit
O(n 2/p) + O(n · log p) ,
die Kosten betragen
O(n 2) + O(p · logp · n) .
Für
p < n/log n ist der Algorithmus kostenoptimal.
) anschließend log p Mischphasen der Zeit
O(n) .
Also beträgt die Gesamtzeit
O(n 2/p) + O(n · log p) ,
die Kosten betragen
O(n 2) + O(p · logp · n) .
Für
p < n/log n ist der Algorithmus kostenoptimal.
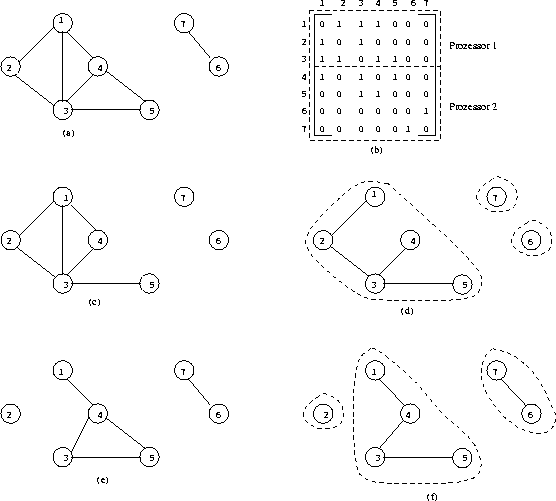
| |
Graph (a) |
Partitionierung der Adjazenzmatrix (b) |
| |
Teilgraph für P1 (c) |
Spannwald berechnet von P1 (d) |
| |
Teilgraph für P2 (e) |
Spannwald berechnet von P2 (f) |
Während des Ablaufs existiert eine Partition der
Knoten in vorläufige Zusammenhangskomponenten.
Jede vorläufige Zusammenhangskomponente wird repräsentiert durch
den an ihr beteiligten Knoten mit der kleinsten Nummer, genannt
Superknoten.
Dieser Knoten ist Vater für alle Knoten der Zusammenhangskomponente,
einschließlich für sich selbst.
In jeder Iteration sucht sich jede unfertige Zusammenhangskomponente
einen Partner und vereinigt sich mit diesem.
Zu Beginn ist jeder Knoten sein eigener Vater und somit Superknoten.
Jede Iteration hat drei Phasen:
| Phase 1: |
Jeder Knoten sucht sich als Freund
den kleinsten benachbarten
Superknoten, d.h. von den Vätern seiner Nachbarn den kleinsten. |
| |
(Dabei wird nach Möglichkeit ein anderer Superknoten gewählt.) |
| Phase 2: |
Jeder Superknoten sucht sich als neuen Vater den kleinsten
Freund seiner Söhne. |
| |
(Dabei wird nach Möglichkeit ein anderer Superknoten gewählt.) |
| Phase 3: |
Jeder Knoten sucht sich als neuen Vater das Minimum
seiner Vorfahren. |
Es wird eine CREW-PRAM mit n 2
Prozessoren verwendet.
Da sich in jeder Iteration
die Anzahl der Zusammenhangskomponenten
mindestens halbiert, entstehen höchstens log (n)
Iterationen.
Jede Iteration benötigt:
Je n Prozessoren bearbeiten Knoten x .
Für alle Knoten, die x zum Nachbarn haben, wird über
ihren Vater minimiert.
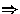 O(log n)
Je n Prozessoren bearbeiten Superknoten x .
O(log n)
Je n Prozessoren bearbeiten Superknoten x .
Für alle Knoten, die x zum Vater haben, wird über
ihren Freund minimiert.
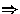 O(log n)
n Prozessoren ersetzen log n mal bei jedem Knoten den Vater durch
den Großvater.
O(log n)
n Prozessoren ersetzen log n mal bei jedem Knoten den Vater durch
den Großvater.
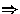 O(log n)
O(log n)
Die Gesamtlaufzeit beträgt daher
O(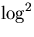 n) ,
die Kosten
O(n 2 ·
n) ,
die Kosten
O(n 2 · 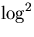 n) .
n) .
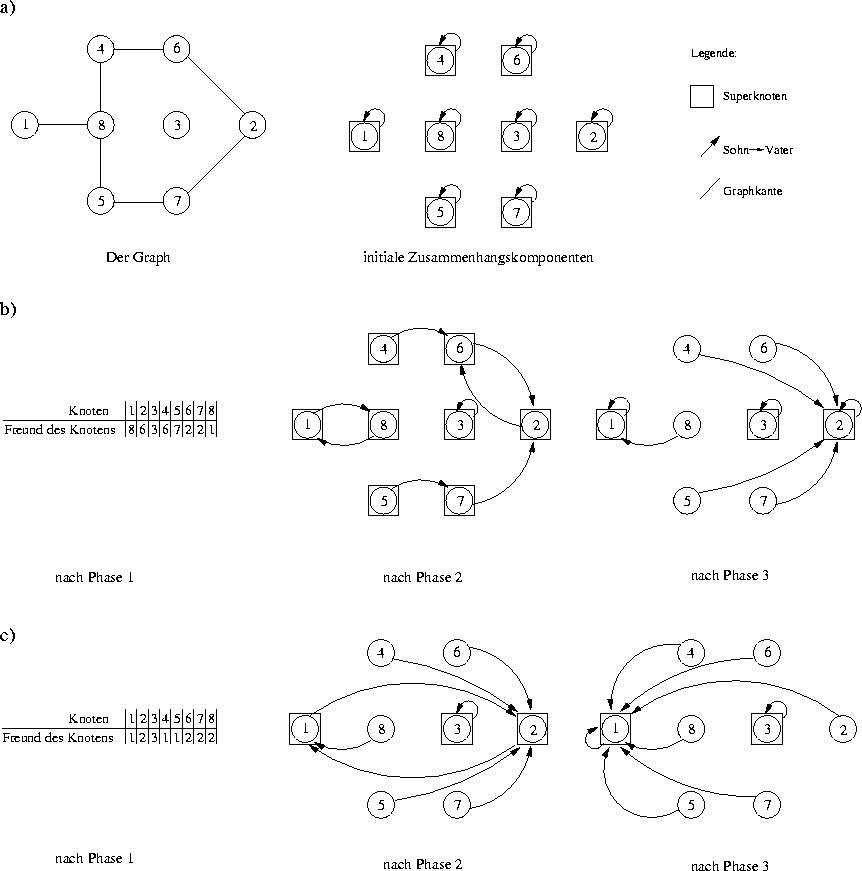
| |
a) Ausgangsgraph |
| |
b) 1. Iteration |
| |
c) 2. Iteration |






