5 Performance

Zur Beurteilung eines parallelen Algorithmus werden verschiedene Maße verwendet.

Sequentialzeit T_s : Zeit zwischen Anfang und Ende der Rechnung auf einem Single-Prozessor-System

Parallelzeit T_p : Zeit zwischen Anfang und Ende der Rechnung auf einem Multiprozessorsystem mit p Prozessoren

Speedup S : T_s/T_p , wobei T_s die Sequentialzeit des besten sequentiellen Algorithmus ist

Effizienz E : S/p

Kosten C : p · T_p

Ein paralleler Algorithmus heißt kostenoptimal, falls seine Kosten proportional zur Sequentialzeit sind.

Beispiel:

Addieren von n Zahlen auf einem Hypercube mit n Prozessoren benötigt Zeit O(log n) gemäß All-to-One-Broadcast im Kapitel 4.2
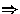$\Rightarrow$ Speedup = O(n/log n)
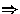$\Rightarrow$ Effizienz = O(1/log n)
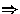$\Rightarrow$ Kosten = O(n · log n)
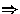$\Rightarrow$ nicht kostenoptimal

Für real existierende Multiprozessorsysteme ist die Anzahl p der Prozessoren fest (und daher unabhängig von n ). Laufzeit, Speedup, Effizienz und Kosten sind daher Funktionen von n und p .

Beispiel: Beim Addieren von n Zahlen auf einem Hypercube mit p Prozessoren werde jeweils ein Zeitschritt benötigt zum Addieren zweier Zahlen und zum Versenden einer Zahl.
Jede der n/p Teilfolgen wird zunächst in n/p - 1 Schritten lokal aufsummiert und dann in log p Phasen mit je einer Kommunikation und einer Addition zusammengeführt. Daraus ergibt sich n/p - 1 + 2 · log p . Für große n,p läßt sich der Term - 1 vernachlässigen. Also gilt

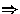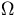$\Rightarrow$ Solange n = $\Omega$(p · log p) , ist der Algorithmus kostenoptimal.

Speedupkurven für verschiedene Problemgrößen beim Addieren im Hypercube

n p = 1 p = 4 p = 8 p = 16 p = 32

64 1.0 0.80 0.57 0.33 0.17

192 1.0 0.92 0.80 0.60 0.38

320 1.0 0.95 0.87 0.71 0.50

512 1.0 0.97 0.91 0.80 0.62

Offenbar fällt die Effizienz mit wachsender Prozessorzahl und steigt mit wachsender Problemgröße. Ein paralleles System heißt skalierbar, wenn sich bei wachsender Prozessorzahl eine konstante Effizienz halten läßt durch geeignetes Erhöhen der Problemgröße.

Beispiel:

Laut Tabelle 5.1 beträgt die Effizienz 0.80 für n = 64 Zahlen und p = 4 Prozessoren. Die Beziehung zwischen Problemgröße und Prozessorzahl lautet n = 8p · log p . Wird die Prozessorzahl auf p = 8 erhöht, muß daher die Problemgröße auf n = 8 · 8 · log 8 = 192 wachsen, um die Effizienz von 80% zu halten.

Um eine Funktion für die Skalierbarkeit zu erhalten, definieren wir zunächst als Problemgröße W die Laufzeit des besten sequentiellen Algorithmus. Die Overheadfunktion T₀ drückt die Differenz zwischen den parallelen und sequentiellen Kosten aus:

T₀(W,p) = p · T_p - W

Zum Beispiel beträgt der Overhead für das Addieren von n Zahlen im Hypercube:

p · (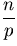$${\frac{n}{p}}$$ + 2 · logp) - n = 2 · p · log p

Durch Umformen erhalten wir:

Daraus folgt:

Zu gegebener Effizienz E ist K = 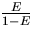${\frac{E}{1-E}}$ eine Konstante, d.h.

Diese Beziehung, genannt Isoeffizienzfunktion, drückt das erforderliche Problemgrößenwachstum in Abhängigkeit von p aus.
Beispiel: Der Overhead für das Addieren im Hypercube beträgt 2 · p · log p . Für E = 0.8 lautet die Isoeffizienzfunktion

Wächst die Prozessorzahl von p auf p' , so muß die Problemgröße um den Faktor

wachsen.

Isoeffizienzfunktion 8p · log p