In Section 3.1.1 we already saw the simplest and original case of an artificial NN, the perceptron, which is viewed as one single neuron. The perceptron receives a vector of inputs, multiplies it with a weight-vector and uses this linear combination to give an classification output of either 0 or 1. In the metaphor of NN the weights just correspond to the strength of each input connection. During ``training'' of the network the strength of the connections are adjusted according to how useful and how ``right'' they are in doing the correct classification.
As we know from section 3.1.1, perceptrons are limited in changing their
decision-surface: all ``adaptations'' of the model still result in a hyperplane.
They are also limited in the number of classes, in that only two classes can be
distinguished. The second problem was overcome just be using one perceptron
for each class with the weighted sums as output. A single neuron in a second layer
then made the classification according to the perceptron with the highest output.
More flexible decision-surfaces could be reached by not only giving the original variables
(in NN often called features) as inputs to the first layer, but by also using the products
![]() of the n input variables
of the n input variables
![]() allowing parabolic decision surfaces.
allowing parabolic decision surfaces.
Creating all these new features can also be seen as another preceding layer of neurons. This NN is then called a ``Quadratic Machine''. We could proceed in this way, creating more and more features out of our variables and reaching the ability to create more and more flexible decision surfaces. The only serious problem is that we get an enormous number of inputs and neurons. This alone is a computational and a storage problem. But the real problem is also that the training requirements increase drastically. All the new connections need to be trained. One heuristic for a good sized training set is that it takes 10 times the number of connections as the number of training entities.
/paragraphBackpropagation MLP: A different approach would be not to precalculate all the different variable-combinations, but instead let the network ``learn'' what connections are important. We would do this by introducing more layers (one is actually enough), each extracting decision making features from the previous layer. Here the problem is how to train the first layers of a multilayer network. The corrent classification for the training data is only available for the last layer, the output classification layer. One solution out of this dilemma is the famous ``backpropagation'' algorithm.
The ``backpropagation'' algorithm is based on continuous and differentiable
transformation functions for each neuron in a network with several layers (MLP).
Each neuron takes the weighted sum of
its inputs (which is continuous and differentiable)
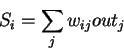 |
(17) |
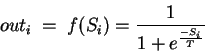 |
(18) |
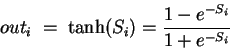 |
(19) |
Because the outi are differentiable we are able to ``backpropagate'' the error. In the reverse order of classification each neuron receives an error feedback from the neurons of the following layer about the partial ``fault'' it has on a misclassification. According to this information each neuron can train and adjust its weights. More detailed information on the background and mathematics of the backpropagation algorithm can be found in [43, pp. 87-95], [48, pp. 122-133], or nearly any other book on NN.