Dritte Normalform

Wir betrachten die Relation

Student : {[ MatrNr, Name, Fachbereich, Dekan]}

Eine mögliche Ausprägung könnte sein:

MatrNr	Name	Fachbereich	Dekan
29555	Feuerbach	6	Matthies
27550	Schopenhauer	6	Matthies
26120	Fichte	4	Kapphan
25403	Jonas	6	Matthies
28106	Carnap	7	Weingarten

Offenbar ist Student in der zweiten Normalform, denn die Nichtprimärattribute Name, Fachbereich und Dekan hängen voll funktional vom einzigen Schlüsselkandidat MatrNr ab.

Allerdings bestehen unschöne Abhängigkeiten zwischen den Nichtprimärattributen, z. B. hängt Dekan vom Fachbereich ab. Dies bedeutet, daß bei einem Dekanswechsel mehrere Tupel geändert werden müssen.

Seien X, Y, Z Mengen von Attributen eines Relationenschemas $\cal {R}$ mit Attributmenge U.
Z heißt transitiv abhängig von X, falls gilt

X $\cap$ Z = $\emptyset$
$\exists$ Y $\subset$ U : X $\cap$ Y = $\emptyset$, Y $\cap$ Z = $\emptyset$
X $\rightarrow$ Y $\rightarrow$ Z, Y $\not\rightarrow$X

Zum Beispiel ist in der Relation Student das Attribut Dekan transitiv abhängig von MatrNr:

MatrNr

$\;\stackrel{\not\leftarrow}{\rightarrow}\;$ Fachbereich $\rightarrow$ Dekan

Ein Relationenschema $\cal {R}$ ist in dritter Normalform falls gilt

• $\cal {R}$ ist in zweiter Normalform
• Jedes Nichtprimärattribut ist nicht-transitiv abhängig von jedem Schlüsselkandidaten.

Graphische Darstellung der funktionalen Abhängigkeiten von ProfessorenAdr

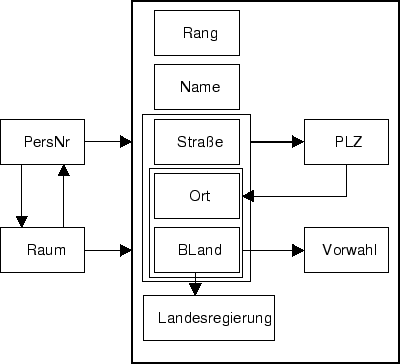
Als Beispiel betrachten wir die bereits bekannte Relation

ProfessorenAdr : {[PersNr, Name, Rang, Raum, Ort, Straße
PLZ, Vorwahl, BLand, Landesregierung]}

Abbildung 11.2 zeigt die funktionalen Abhängigkeiten in der graphischen Darstellung. Offenbar ist die Relation nicht in der dritten Normalform, da das Nichtprimärattribut Vorwahl transitiv abhängig vom Schlüsselkandidaten PersNr ist:

PersNr$\;\stackrel{\not\leftarrow}{\rightarrow}\;$ { Ort, BLand } $\rightarrow$ Vorwahl

Um Relationen in dritter Normalform zu erhalten, ist häufig eine starke Aufsplittung erforderlich. Dies führt natürlich zu erhöhtem Aufwand bei Queries, da ggf. mehrere Verbundoperationen erforderlich werden.