Es werden diejenigen Tupel ausgewählt, die das Selektionsprädikat
erfüllen. Die Selektion wird mit ![]() bezeichnet und hat
das Selektionsprädikat als Subskript.
bezeichnet und hat
das Selektionsprädikat als Subskript.
Die Projektion
liefert als Ergebnis
| MatNr | Name | Semester |
| 24002 | Xenokrates | 18 |
| 25403 | Jonas | 12 |
Das Selektionsprädikat wird beschrieben durch eine Formel F mit folgenden Bestandteilen:
- Attributnamen der Argumentrelation R oder Konstanten als Operanden
- arithmetische Vergleichsoperatoren
< = >
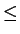
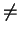
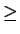
- logische Operatoren:
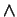
 (und oder nicht)
(und oder nicht)
Bei der Projektion werden Spalten der Argumentrelation extrahiert.
Das Operatorsymbol lautet ![]() , die gewünschten Attribute
werden im Subskript aufgelistet:
, die gewünschten Attribute
werden im Subskript aufgelistet:
liefert als Ergebnis
| Rang |
| C4 |
| C3 |
Die Attributmenge wird üblicherweise nicht unter Verwendung von Mengenklammern sondern als durch Kommata getrennte Sequenz gegeben. Achtung: Da das Ergebnis wiederum eine Relation ist, existieren per definitionem keine Duplikate ! In der Praxis müssen sie dennoch algorithmisch entfernt werden.
Zwei Relationen mit gleichem Schema können durch die
Vereinigung, symbolisiert durch ![]() , zusammengefaßt werden.
Beispiel:
, zusammengefaßt werden.
Beispiel:
Für zwei Relationen R und S mit gleichem Schema ist die Mengendifferenz R - S definiert als die Menge der Tupel, die in R aber nicht in S vorkommen. Beispiel
liefert die Matrikelnummern derjenigen Studenten, die noch nicht geprüft wurden.
Das kartesische Produkt (Kreuzprodukt) zweier Relationen R und S wird mit R x S bezeichnet und enthält alle möglichen Paare von Tupeln aus R und S. Das Schema der Ergebnisrelation, also sch (R x S), ist die Vereinigung der Attribute aus sch(R) und sch(S).
Das Kreuzprodukt von Professoren und hören hat 6 Attribute und enthält 91 (= 7 . 13) Tupel.
| PersNr | name | Rang | Raum | MatNr | VorlNr |
| 2125 | Sokrates | C4 | 226 | 26120 | 5001 |
| ... | ... | ... | ... | ... | ... |
| 2125 | Sokrates | C4 | 226 | 29555 | 5001 |
| ... | ... | ... | ... | ... | ... |
| 2137 | Kant | C4 | 7 | 29555 | 5001 |
Haben beide Argumentrelationen ein gleichnamiges Attribut A, so kann dies durch Voranstellung des Relationennamen R in der Form R.A identifiziert werden.
Zum Umbenennen von Relationen und Attributen wird der Operator
![]() verwendet, wobei im Subskript entweder der neue
Relationenname steht oder die Kombination
von neuen und altem Attributnamen durch einen Linkspfeil getrennt. Beispiele:
verwendet, wobei im Subskript entweder der neue
Relationenname steht oder die Kombination
von neuen und altem Attributnamen durch einen Linkspfeil getrennt. Beispiele:
Eine Umbenennung kann dann erforderlich werden, wenn durch das kartesische Produkt Relationen mit identischen Attributnamen kombiniert werden sollen.
Als Beispiel betrachten wir das Problem, die Vorgänger der Vorgänger der Vorlesung mit der Nummer 5216 herausfinden. Hierzu ist ein kartesisches Produkt der Tabelle mit sich selbst erforderlich, nachdem zuvor die Spalten umbenannt worden sind:
Die konstruierte Tabelle hat vier Spalten und enthält das Lösungstupel mit dem Wert 5001 als Vorgänger von 5041, welches wiederum der Vorgänger von 5216 ist:
| Vorgänger | Nachfolger | Vorgänger | Nachfolger |
| 5001 | 5041 | 5001 | 5041 |
| ... | ... | ... | ... |
| 5001 | 5041 | 5041 | 5216 |
| ... | ... | ... | ... |
| 5052 | 5259 | 5052 | 5259 |
Der sogenannte natürliche Verbund zweier Relationen R
und S wird mit
R ![]() S gebildet. Wenn R insgesamt
m + k Attribute
A1,..., Am, B1,..., Bk
und S insgesamt n + k Attribute
B1,..., Bk, C1,..., Cn
hat, dann hat
R
S gebildet. Wenn R insgesamt
m + k Attribute
A1,..., Am, B1,..., Bk
und S insgesamt n + k Attribute
B1,..., Bk, C1,..., Cn
hat, dann hat
R ![]() S die Stelligkeit m + k + n.
Hierbei wird vorausgesetzt, daß die Attribute Ai und Cj jeweils
paarweise verschieden sind. Das Ergebnis von
R
S die Stelligkeit m + k + n.
Hierbei wird vorausgesetzt, daß die Attribute Ai und Cj jeweils
paarweise verschieden sind. Das Ergebnis von
R ![]() S ist definiert als
S ist definiert als
Es wird also das kartesische Produkt gebildet, aus dem nur diejenigen Tupel selektiert werden, deren Attributwerte für gleichbenannte Attribute der beiden Argumentrelationen gleich sind. Diese gleichbenannten Attribute werden in das Ergebnis nur einmal übernommen.
Die Verknüpfung der Studenten mit ihren Vorlesungen geschieht durch
Das Ergebnis ist eine 7-stellige Relation:
| MatrNr | Name | Semester | VorlNr | Titel | SWS | gelesenVon |
| 26120 | Fichte | 10 | 5001 | Grundzüge | 4 | 2137 |
| 25403 | Jonas | 12 | 5022 | Glaube und Wissen | 2 | 2137 |
| 28106 | Carnap | 3 | 4052 | Wissenschaftstheorie | 3 | 2126 |
| ... | ... | ... | ... | ... | ... | ... |
Da der Join-Operator assoziativ ist, können wir auch auf die Klammerung verzichten und einfach schreiben
Wenn zwei Relationen verbunden werden sollen bzgl. zweier
Attribute, die zwar die gleiche Bedeutung aber unterschiedliche
Benennungen haben, so müssen diese vor dem Join
mit dem ![]() -Operator
umbenannt werden. Zum Beispiel liefert
-Operator
umbenannt werden. Zum Beispiel liefert
die Relation {[VorlNr, Titel, SWS, gelesenVon, Name, Rang, Raum]}
Beim natürlichen Verbund müssen die Werte der gleichbenannten
Attribute übereinstimmen. Der allgemeine Join-Operator,
auch Theta-Join genannt, erlaubt die Spezifikation
eines beliebigen Join-Prädikats ![]() .
Ein Theta-Join
R
.
Ein Theta-Join
R ![]() S über
der Relation R mit den Attributen
A1, A2,..., An
und der Relation S mit den Attributen
B1, B2,..., Bn
verlangt die Einhaltung des Prädikats
S über
der Relation R mit den Attributen
A1, A2,..., An
und der Relation S mit den Attributen
B1, B2,..., Bn
verlangt die Einhaltung des Prädikats ![]() , beispielsweise in
der Form
, beispielsweise in
der Form
Das Ergebnis ist eine n + m-stellige Relation und läßt sich auch als Kombination von Kreuzprodukt und Selektion schreiben:
Wenn in der Universitätsdatenbank die Professoren und die Assistenten um das Attribut Gehalt erweitert würden, so könnten wir diejenigen Professoren ermitteln, deren zugeordnete Assistenten mehr als sie selbst verdienen:
Die bisher genannten Join-Operatoren werden auch innere Joins genannt ( inner join). Bei ihnen gehen diejenigen Tupel der Argumentrelationen verloren, die keinen Join-Partner gefunden haben. Bei den äußeren Join-Operatoren ( outer joins) werden - je nach Typ des Joins - auch partnerlose Tupel gerettet:
- left outer join: Die Tupel der linken Argumentrelation bleiben erhalten
- right outer join: Die Tupel der rechten Argumentrelation bleiben erhalten
- full outer join: Die Tupel beider Argumentrelationen bleiben erhalten
Somit lassen sich zu zwei Relationen L und R insgesamt vier verschiedene Joins konstruieren:
![\begin{figure}
\begin{center}
\begin{tabular}{ccc}
\begin{tabular}[t]{\vert c\ve...
...$\ & $d_2$\ & $e_2$\\
\hline
\end{tabular}\end{tabular}\end{center}\end{figure}](img55.gif)
Der Mengendurchschnitt (Operatorsymbol ![]() )
ist anwendbar auf zwei Argumentrelationen
mit gleichem Schema. Im Ergebnis liegen alle Tupel, die in beiden
Argumentrelationen liegen. Beispiel:
)
ist anwendbar auf zwei Argumentrelationen
mit gleichem Schema. Im Ergebnis liegen alle Tupel, die in beiden
Argumentrelationen liegen. Beispiel:
liefert die Personalnummer aller C4-Professoren, die mindestens eine Vorlesung halten.
Der Mengendurchschnitt läßt sich mithilfe der Mengendifferenz bilden:
Sei R eine r-stellige Relation, sei S eine s-stellige Relation, deren Attributmenge in R enthalten ist.
Mit der Division
sind alle die Anfangsstücke von R gemeint, zu denen sämtliche Verlängerungen mit Tupeln aus S in der Relation R liegen. Beispiel:
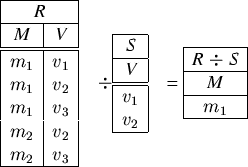
Die Division von R durch S läßt sich schrittweise mithilfe der unabhängigen Operatoren nachvollziehen (zur Vereinfachung werden hier die Attribute statt über ihre Namen über ihren Index projiziert):
|
T : = |
alle Anfangsstücke |
| T x S | diese kombiniert mit allen Verlängerungen aus S |
| (T x S)\R | davon nur solche, die nicht in R sind |
|
V : = |
davon die Anfangsstücke |
| T\V | davon das Komplement |