Rotation um die ![]() -Achse
-Achse
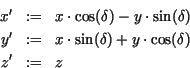
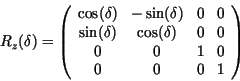
Rotation um die ![]() -Achse
-Achse
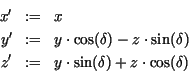
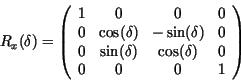
Rotation um die ![]() -Achse
-Achse
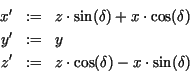
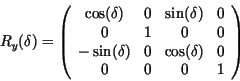
Rotation um eine beliebige Achse
Voraussetzung: Die Rotationsachse stimme nicht mit einer der Koordinatenachsen überein.
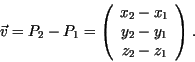
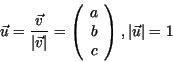
Für Schritt 2 sind Sinus und Cosinus des Rotationswinkels
![]() erforderlich, der zwischen der Projektion
erforderlich, der zwischen der Projektion ![]() von
von ![]() auf die
auf die ![]() -Fläche und der
-Fläche und der ![]() -Achse, repräsentiert durch
den Vektor
-Achse, repräsentiert durch
den Vektor
![]() , liegt.
, liegt.

![]()
![]()
Nach Schritt 2 befindet sich der ursprüngliche Vektor ![]() als
als
![]() in der
in der ![]() -Ebene:
-Ebene:
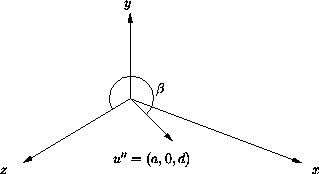
Für Schritt 3 (Rotation um ![]() -Achse) benötigt man
Sinus und Cosinus des Rotationswinkels
-Achse) benötigt man
Sinus und Cosinus des Rotationswinkels ![]() . Positive Winkel ergeben
eine Rotation gegen den Uhrzeigersinn, wenn man aus Richtung der Positiven
. Positive Winkel ergeben
eine Rotation gegen den Uhrzeigersinn, wenn man aus Richtung der Positiven
![]() -Achse auf die
-Achse auf die ![]() -Ebene schaut:
-Ebene schaut:
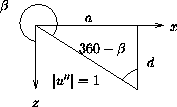
![]()
![]()
Nach den ersten drei Schritten ist die Drehachse mit der ![]() -Achse
identisch, so daß Schritt (4) mit der Rotationsmatrix
-Achse
identisch, so daß Schritt (4) mit der Rotationsmatrix ![]() durchgeführt werden kann.
Schritt (5) beinhaltet die Anwendung der inversen Transformationen.
durchgeführt werden kann.
Schritt (5) beinhaltet die Anwendung der inversen Transformationen.
Die Rotation um die Achse
![]() um den Winkel
um den Winkel ![]() läßt sich daher
wie folgt darstellen:
läßt sich daher
wie folgt darstellen: