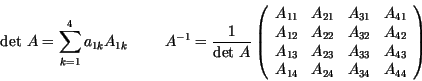Analog zum zweidimensionalen Fall werden die dreidimensionalen
Transformationen durch Verknüpfung homogener Koordinaten
mit ![]() -Transformationsmatrizen dargestellt.
-Transformationsmatrizen dargestellt.
Sei ![]() ,
,
![]() , eine
, eine ![]() -Matrix:
-Matrix:
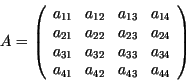
Ist
![]() die Determinante von
die Determinante von ![]() ,
so bezeichnet man als Unterdeterminante des Elementes
,
so bezeichnet man als Unterdeterminante des Elementes
![]() diejenige 3-reihige Determinante,
die aus
diejenige 3-reihige Determinante,
die aus ![]() durch Streichen der
durch Streichen der ![]() -ten Zeile und der
-ten Zeile und der ![]() -ten Spalte
hervorgeht.
Unter der Adjunkten
-ten Spalte
hervorgeht.
Unter der Adjunkten ![]() des Elementes
des Elementes ![]() versteht man die mit dem Faktor
versteht man die mit dem Faktor ![]() versehene Unterdeterminante von
versehene Unterdeterminante von ![]() .
.
Beispiel:
![\begin{displaymath}
A_{23} = - \left\vert \begin{array}{ccc}
a_{11} & a_{12} & a...
...{44} - a_{34}
a_{41}) + a_{14}(a_{31} a_{42} - a_{32} a_{41})]
\end{displaymath}](img479.gif)
Die Adjunkten sind nützlich zur Berechnung der Determinanten von ![]() sowie
der inversen Matrix
sowie
der inversen Matrix ![]() (sofern diese existiert!):
(sofern diese existiert!):