Koordinatensysteme

Das geläufigste Koordinatensystem für die oben genannte euklidische Ebene ($\mathbb{R}$) ist das kartesische Koordinatensystem. Seine beiden Koordinatenachsen sind senkrecht zueinander und schneiden sich im (willkürlich festgelegten) Ursprung $O$. Die beiden Einheitsvektoren $\vec{e}_x$ und $\vec{e}_y$ sind parallel zu den Achsen und führen, wenn sie von $O$ abgetragen werden, zu den Punkten mit Abstand $1$ von $O$. Als Spaltenvektoren geschrieben, haben sie folgendes Aussehen:

$$\vec{e}_x = \left( \begin{array}{c} 1 \\ 0 \end{array} \righ... ...vec{e}_y = \left( \begin{array}{c} 0 \\ 1 \end{array} \right)$$

Aus Platzgründen wird stellenweise die Schreibweise als Zeilenvektor verwendet:

$$\vec{e}_x = (1 \;\; 0)^T ; \; \; \vec{e}_y = (0 \;\; 1)^T$$

Die erste Koordinatenachse ($x$-Achse) wird immer von links nach rechts gezeichnet; d.h. die größeren Koordinatenwerte befinden sich weiter rechts.

An der Tafel bzw. in der Vorlesung wird für gewöhnlich die 2. Koordinatenachse ($y$-Achse) so gezeichnet, daß die größeren Werte weiter oben sind.

Auf dem Bildschirm hingegen befindet sich der Ursprung $O$ oben links; d.h. die $y$-Achse liegt so, daß sich die größeren Koordinatenwerte weiter unten befinden. Insbesondere hat kein Bildschirmpunkt negative Koordinaten.

Kartesisches Koordinatensystem an der Tafel

Kartesisches Koordinatensystem am Bildschirm

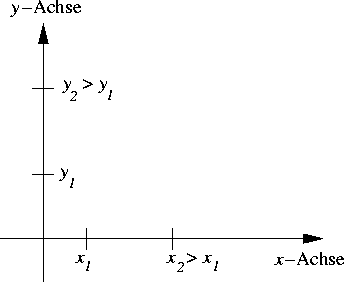
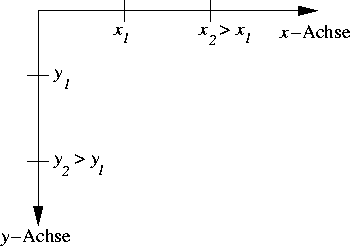
Andere Koordinatensysteme und der Wechsel zwischen diesen werden später ausführlich behandelt.