Anwendung des Kreuzprodukts

Gegeben sei eine Fläche durch 3 nicht kollineare Punkte P₁,P₂,P₃ .

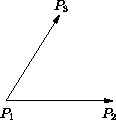
Der Vektor (P₂ - P₁) × (P₃ - P₁) bildet den Normalenvektor zur Fläche.
Ist eine Ebene durch ihre Ebenengleichung Ax + By + Cz + D = 0 gegeben, so ergibt sich der Normalenvektor als (A,B,C) .
Ist ein Normalenvektor (A,B,C) gegeben, so errechnet sich D durch Einsetzen eines beliebigen Punktes der Ebene.
Ein Punkt (x,y,z) liegt

oberhalb der Ebene, falls Ax + By + Cz + D > 0

unterhalb der Ebene, falls Ax + By + Cz + D < 0

in der Ebene, falls Ax + By + Cz + D = 0