public class Komplex
{
double re;
double im;
...
Das Quadrat einer komplexen Zahl z hat den
Realteil
z.re 2 - z.im 2 und den Imaginärteil
2 · z.re · z.im .
Der Betrag einer komplexen Zahl c sei
|c| = ![]() .
.
Betrachte die Funktion
f : ![]()
![]()
![]() ,f (z) = z 2 + c
für festes c .
,f (z) = z 2 + c
für festes c .
Komplex f(Komplex z)
{
double tmp;
tmp = z.re;
z.re = z.re * z.re - z.im * z.im + c.re;
z.im = 2 * tmp * z.im + c.im;
return z
}
Betrachte die Folge
z,f (z),f 2(z),f 3(z),...
beginnend bei z = 0 für festes c .
Für manche c wächst der Betrag beliebig,
für manche c konvergiert er zu einem Fixpunkt.
Die
Mandelbrotmenge besteht aus solchen komplexen Zahlen c , die beim
Startwert z = 0 zur Konvergenz führen.
Um die Mandelbrotmenge grafisch darzustellen, definiert man
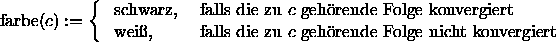
Ordne jedem Pixel (p.x,p.y) des Bildschirms eine komplexe Zahl
zu wie folgt. Die linke obere Ecke bezeichne die komplexe Zahl
start
(z.B. - 2.15,2.15 ).
Die rechte obere Ecke bezeichne die komplexe Zahl ende
(z.B. 0.85,2.15 )
Dann ergibt sich bei 300 Pixeln pro Zeile eine Schrittweite von
(0.85 + 2.15)/300 = 0.01 .
Somit läßt sich ein Koordinatenpaar (p.x,p.y) umrechnen durch den folgenden
Konstruktor.
public Komplex(Point p, Komplex start, double schritt)
// bildet die komplexe Zahl zum Pixel p mit linker/oberer Ecke start
// und Schrittweite schritt
{
this.re = start.re + schritt * (double)p.x;
this.im = start.im - schritt * (double)p.y;
}
Sei (p.x,p.y) das zur komplexen Zahl c gehörende Pixel. Dann färbe es mit farbe( c ).

Implementation der Mandelbrot-Menge
Sobald während des Iterierens der Betrag von
z > 2 ![]() Folge konvergiert definitiv nicht.
Folge konvergiert definitiv nicht.
Falls Betrag von z nach z.B. 100 Iterationen noch
< 2 ![]() Folge konvergiert vermutlich.
Folge konvergiert vermutlich.
D.h., bei Erreichen einer vorgegebenen Iterationenzahl wird das Pixel,
welches der komplexen Zahl c entspricht, schwarz gefärbt, da c
vermutlich zur Konvergenz führt.
void mandel ()
{
Point p;
int zaehler;
Komplex c, z;
for (p.x = 0; p.x < WIDTH; p.x++)
for (p.y = 0; p.y < HEIGHT; p.y++)
{
zaehler = 0;
c = new Komplex(p, start, schritt);
z = new Komplex(c);
while ((betrag (z) < 2.0) && (zaehler++ < max_iter))
z = f(z);
if (betrag(z) < 2.0) set_pixel(p);
}
}

Also ergibt sich:
if (betrag < 2.0) set_pixel (p); else
if ((zaehler % 2) != 0) set_pixel (p);
Bei Farbbildschirmen gibt es folgende Möglichkeit, die Divergenzgeschwindigkeit der Folge für ein c zu veranschaulichen:
Es seien die Farben
farbe[0], ..., farbe[NUM_COL-1]
vorhanden
set_col_pixel (p, farbe [zaehler % NUM_COL])

/************************************************************************************/
/* Mandelbrotmenge */
/************************************************************************************/
void mandel( // berechnet und zeichnet Mandelbrotmenge ab
Komplex start, // linker oberer Ecke start der komplexen Flaeche
double schritt, // mit Schrittweite schritt und
int max_iter, // Iterationsanzahl max_iter (muss gerade sein)
int fall) // gemaess Fall fall
// Abbruch, wenn Quadrat des Betrags >= 4
// oder wenn Iterationszahl erreicht ist
{
Komplex c = new Komplex(0.0, 0.0);
Komplex z = new Komplex(0.0, 0.0);
Point p = new Point();
double q_betrag, tmp;
int zaehler ;
for (p.x = 0, c.re = start.re; p.x < WIDTH; p.x++, c.re += schritt)
for (p.y = 0, c.im = start.im; p.y < HEIGHT; p.y++, c.im += schritt)
{
z.re = 0.0;
z.im = 0.0;
zaehler = 0;
q_betrag = 0.0;
while( (q_betrag < 4.0) && (zaehler++ < max_iter) ) {
tmp = z.re;
z.re = z.re * z.re - z.im * z.im + c.re;
z.im = 2 * tmp * z.im + c.im;
q_betrag = z.re*z.re + z.im*z.im;
}
switch (fall) {
case 1: if (q_betrag(z) < 4.0) set_pixel(p); break; // schwarz
case 2: if (q_betrag(z) < 4.0) set_pixel(p); else // schwarz
if ((zaehler %2) != 0) set_pixel(p); break; // mit modulo
case 3: if(zaehler == max_iter+1)
set_col_pixel(p,farbe[0]); else // Mandelbrotmenge
set_col_pixel(p,farbe[zaehler%NUM_COL]); break; // farbe modulo
}
}
}
|