7.4 B-Splines

Es sollen nun nicht alle Stützpunkte Einfluß auf den gesamten Kurvenverlauf haben und der Grad der Polynome soll unabhängig von der Zahl der Stützpunkte sein.

Spezifiziere die Kurve durch n + 1 Stützpunkte P₀,...,P_n und einen Knotenvektor
T = (t₀,t₁,...,t_{n + k}),t_j t_{j + 1} .

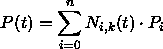
Die Punkte P_i wirken sich nur auf maximal k Kurvenabschnitte aus und werden gewichtet durch die Basis des B-Splines, Polynome N_i,k(t) vom Grad k - 1 ( 0 i n ) :

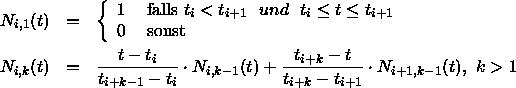
Bei Division durch Null wird der Quotient gleich 0 gesetzt.
Der Knotenvektor wird häufig wie folgt gewählt für 0 j n + k :

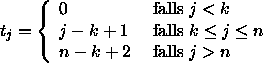
Hierdurch wird t im Intervall [0,n - k + 2] definiert.

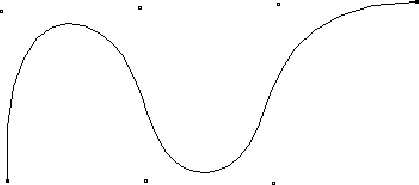
Beispiel: k = 3 , n = 4 ergibt einen uniformen quadratischen B-Spline mit dem Knotenvektor T = (0,0,0,1,2,3,3,3) . Die Stützpunkte P₀,P₁,P₂,P₃,P₄ haben nur lokal Einfluß auf den Kurvenverlauf, und zwar in den Intervallen t [0,1],[0,2],[0,3],[1,3],[2,3] .

Verlauf der Gewichtungspolynome N_i,k für k = 3

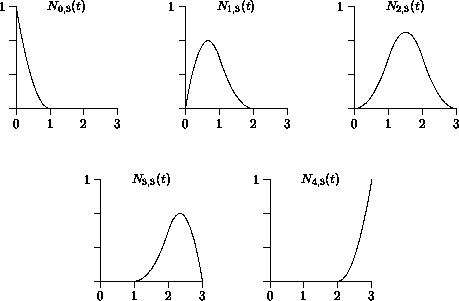
Sonderfall

Für k = n + 1 ergibt sich für den Knotenvektor der Sonderfall

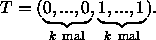
Die zugehörigen B-Splinefunktionen haben die schon bekannte Form

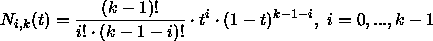
Somit lassen sich also die B-Splinefunktionen als Verallgemeinerung der Bernsteinpolynome auffassen.

Wie bei den Bernsteinpolynomen gilt auch für die B-Splinefunktionen N_i,k , daß sie positiv sind, und N_i,k = 1.

B-Spline mit n = 6 , k = 4 und 35 Interpolationspunkten