7.2 Splines

Gegeben n Stützpunkte. Wähle n - 1 Kurven kleiner Ordnung für den Verlauf innerhalb der n - 1 Intervalle.

Kurven erster Ordnung (Geraden) ergeben nur den Linienzug.

Kurven zweiter Ordnung (Parabeln) sind an den Intervallgrenzen nur einmal differenzierbar.

Kurven dritter Ordnung mit stetigen ersten und zweiten Ableitungen an den Intervallgrenzen (kubische Splines) können zu einer Gesamtkurve mit weichen Übergängen an den Nahtstellen zusammengesetzt werden.

Gesucht:

Approximation einer Kurve f (t) , die durch n vorgegebene Punkte laufen soll.

Bemerkung:

f ist in parametrischer Form gegeben (d.h. x = g(t),y = h(t) ), da die explizite Form y = f (x) pro x -Wert nur einen y -Wert erlaubt.

Die n Stützpunkte seien f (t_i) , die resultierenden Intervalle seien [t_i,t_{i + 1}] , die für das Intervall i zuständige Funktion sei f_i(t) , 1 i n - 1 .

Jedes f_i hat die Form

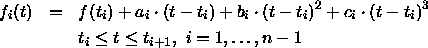
Es muß gelten

f_i(t_{i + 1}) = f_{i + 1}(t_{i + 1}) für i = 1,...,n - 2 gleicher Wert

f_i'(t_{i + 1}) = f_{i + 1}'(t_{i + 1}) für i = 1,...,n - 2 gleiche Steigung

f_i''(t_{i + 1}) = f_{i + 1}''(t_{i + 1}) für i = 1,...,n - 2 gleiche Steigungsänderung

Nach Vorgabe von a₁ und a_{n - 1} entsteht ein Gleichungssystem mit n - 2 Gleichungen und n - 2 Unbekannten a₂,a₃,...,a_{n - 2} .

Die Werte von a₁ und a_{n - 1} können z.B. ermittelt werden durch Festlegung f''(t₁) = f''(t_n) = 0 (natürliche Spline-Interpolation).

Für die Folge t_i reicht jede monoton wachsende Folge. Geeignet ist z.B. die Folge der euklidischen Abstände zwischen den Stützpunkten. Statt den Abstand d = zu berechnen, verwendet man die Näherungsformel · (dx + dy + 2 · max (dx,dy)) .

Vom Spline-Algorithmus erzeugte Kurveninterpolation

/*************************************************************************************/
/*               Spline-Interpolation durch Polynome 3. Grades                       */
/*************************************************************************************/

private static double[] calcfx = new double[MAX_POINTS];       	// x-Funktionswerte
private static double[] calcfy = new double[MAX_POINTS];       	// y-Funktionswerte
private static double[] x = new double[MAX_POINTS];  // x-Koordinaten der Stuetzpunkte
private static double[] y = new double[MAX_POINTS];  // y-Koordinaten der Stuetzpunkte
private static double[] t = new double[MAX_POINTS];  // t-Werte der Stuetzpunkte

void besetze_arrays(                          // berechnet Intervallgrenzen
              int point_cnt,                  // Anzahl der Polygonpunkte
              Point punkt[])                  // Punktliste
{
      int i;
      double ax,ay,dd;
 
      for (i=0; i ay) dd = dd+2*ax;      // Naeherungsformel fuer Euklid:
                      else dd = dd+2*ay;      // Abstand = 1/3*(dx+dy+2*max{dx,dy})
              t[i] = t[i-1]+dd/3;
      }
}
 


void curve_fitting(                         // berechnet die Approximation der Kurve
      int point_cnt,                        // fuer point_cnt Stuetzpunkte
      Point punkt[],                        // uebergeben im Array punkt
      int spline_size)                      // fuer spline_size Interpolationswerte
{
      int i,n=0;
      besetze_arrays(point_cnt, punkt);               // erzeuge Intervallgrenzen und
                                                      // Gleitkommaversion von punkt
      cubic_spline(point_cnt, t, x, spline_size, calcfx);  // bestimme Interpol.werte
      cubic_spline(point_cnt, t, y, spline_size, calcfy);  // bestimme Interpol.werte
      for (i=0; i=0; i--) a[i] = (k[i]-delta_t[i]*a[i+1])/m[i];
      for (i=1; i