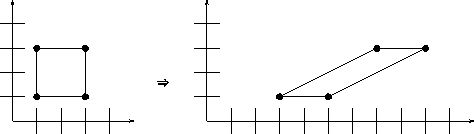Weitere Transformationen, die sich durch Matrizen darstellen lassen, sind
- Spiegelung an einer beliebigen Geraden,
- Spiegelung an einem Punkt,
- Scherung.
Bei der Scherung in x bleiben die y -Werte konstant, und die
x -Werte werden proportional zu den
y -Werten horizontal verschoben, d.h.
x' = x + Schx · y .
Die Transformationsmatrix lautet:

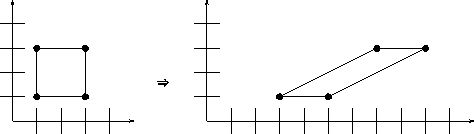
Scherung mit Schx = 2