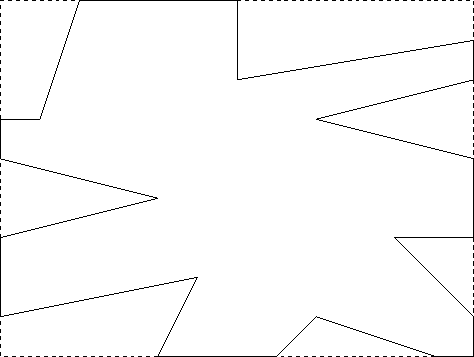
Vielmehr müssen zusätzlich die Ein- und Austrittspunkte verbunden werden, um nach dem Clipping wieder ein Polygon zu erhalten:
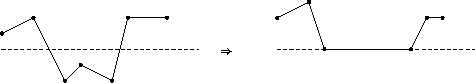
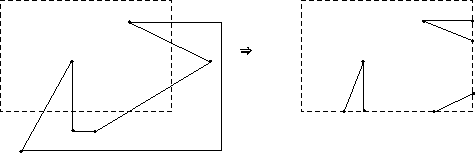
Obacht: Bzgl. der Ecken des Clip-Windows ist eine Spezialbehandlung erforderlich:
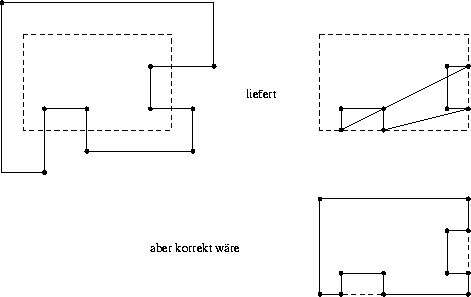
Der Sutherland & Hodgman-Algorithmus clippt an vier Fensterkanten nacheinander:
fuer jede Clipping-Gerade E tue:
fuer jeden Polygonpunkt P tue:
falls P sichtbar: uebernimm ihn
falls Kante von P zu seinem Nachfolger E schneidet:
uebernimm den Schnittpunkt
/****************************************************************************************/
/* */
/* Clippen von Polygonen an einem Fenster nach Sutherland-Hodgmann */
/* */
/****************************************************************************************/
private boolean On_Visible_Side( /* liefert true, falls */
Point P, /* Punkt p auf der sichtbaren */
int wert, /* Seite der Kante wert liegt */
int fall) /* gemaess Fall fall */
{
switch (fall) {
case 0: return (P.x >= wert); /* linke Fenster-Kante */
case 1: return (P.y >= wert); /* untere Fenster-Kante */
case 2: return (P.x <= wert); /* rechte Fenster-Kante */
case 3: return (P.y <= wert); /* obere Fenster-Kante */
}
return false;
}
private boolean Intersection( /* liefert true, */
Point P1, Point P2, /* falls sich die Linie P1-P2 */
int wert, /* mit Clipping-Kante wert schneidet */
int fall, /* gemaess Fall fall */
Point I) /* liefert den Schnittpunkt I zurueck */
{
boolean P1_vis, P2_vis; /* true, falls P1 bzw P2 sichtbar */
double slope; /* Steigung der Geraden P1-P2 */
/* y = (x-P1.x)*slope + P1.y */
P1_vis = On_Visible_Side(P1,wert,fall); /* P1 sichtbar ? */
P2_vis = On_Visible_Side(P2,wert,fall); /* P2 sichtbar ? */
if ((P1_vis && P2_vis) || (!P1_vis && !P2_vis)) return (false);/*kein Schnittpkt*/
else
{
slope = (double)(P2.y-P1.y) / (double) (P2.x-P1.x); /* Steigung */
if (fall%2==1) {
I.x = (int)((wert-P1.y) / slope) + P1.x;
I.y = wert;
} else
{
I.x = wert;
I.y = (int)((wert-P1.x) * slope) + P1.y;
}
return(true);
}
}
private int sutherland_hodgman( /* fuehrt ein Clipping durch */
int num_points, /* fuer num_points Punkte */
Point[] points, /* der Polygonliste Points */
int wert, /* bezueglich Clipping-Kante wert */
int fall) /* gemaess Fall fall */
/* liefert neue Anzahl Punkte */
{
int i;
int old_ptr = 0;
int new_ptr = 0;
Point S, I;
Point[] hpoints = new Point[MAX_POINTS];
if (num_points > 2) {
points[num_points] = points[0];
while (old_ptr < num_points) {
S = points[old_ptr++];
if (On_Visible_Side(S,wert,fall)) hpoints[new_ptr++] = S;
I = new Point();
if (Intersection(S,points[old_ptr],wert,fall,I)) hpoints[new_ptr++] = I;
}
for (i=0; i<new_ptr; i++) points[i]=hpoints[i];
return new_ptr;
}