x 1;0 y 1;0 z 1)
umgewandelt.
Anstelle mehrerer unterschiedlicher Projektionen muß so anschließend nur
noch die orthogonale Parallelprojektion auf die Ebene z = 0
durchgeführt werden.
Das sogenannte View Mapping wird deshalb auch als Ausgabe
auf einen normierten Bildschirm bezeichnet.
Das Koordinatensystem, in dem sich der Einheitswürfel befindet, heißt
Normalized Projection Coordinate System (NPC).
Der Betrachterstandpunkt befindet sich im Unendlichen auf der
positiven z -Achse und hat die homogenen Koordinaten
(0,0,1,0) .
Vom Betrachter
aus gesehen liegt im NPC der Punkt (0,0,0) ``links unten hinten'' und
(1,1,1) ``rechts oben vorne''.
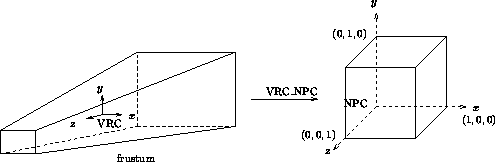
Bei der perspektivischen Projektion wird in einem ersten Schritt der Pyramidenstumpf, der den Bildraum darstellt und frustum genannt wird, auf einen regelmäßigen Pyramidenstumpf abgebildet. Dessen Grundfläche ist ein Quadrat, das mit jeder Seitenfläche einen Winkel von 45 o einschließt. Dabei werden die z -Koordinaten nicht und die x - und y -Koordinaten proportional zur z -Koordinate verändert, was einer Scherung an der z -Achse entspricht. Im zweiten Schritt wird der regelmäßige Pyramidenstumpf in den normierten Einheitswürfel transformiert. Dazu müssen die x - und y -Koordinaten proportional zu den reziproken z -Werten skaliert werden. Die Front Plane entspricht im NPC der Ebene z = 1 und die Back Plane der Ebene z = 0 .
Beide Schritte werden im Programm zu einer Transformationsmatrix zusammengefaßt. Bei deren Anwendung auf die homogenen Koordinaten ist zu beachten, daß die resultierenden Punkte im allgemeinen w -Werte ungleich 1 haben, die affinen Koordinaten also erst nach der Division durch w vorliegen. Außerdem ist diese Abbildung nur bezüglich der x - und y -Koordinaten linear. In z -Richtung werden die Werte durch die Scherung im zweiten Schritt reziprok verzerrt, d.h., äquidistante Punkte längs der z -Achse im VRC häufen sich im NPC bei z = 0 nahe der Back Plane.
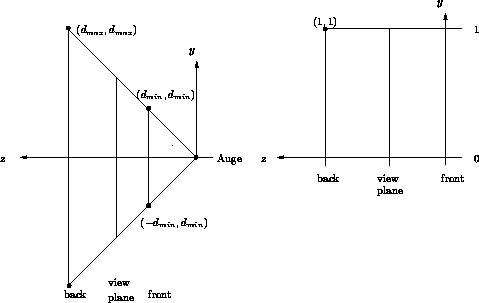
Zur Erleichterung der Herleitung wird zunächst das Koordinatensystem so transformiert, daß der PRP im Ursprung sitzt. Danach wird das Koordinatensystem an der xy -Ebene gespiegelt, indem die z -Koordinaten mit -1 multipliziert werden. Danach ist das Koordinatensystem linkshändig. Es seien dmin,d,dmax die Abstände der Frontplane, Bildebene, Backplane vom Augenpunkt.
Zur Durchführung von Punkt 3.) der Viewing Pipeline wird zunächst die abgeschnittene Pyramide (= frustum) transformiert in einen symmetrischen Pyramidenstumpf mit quadratischer Grundfläche und Kanten unter 45 o .
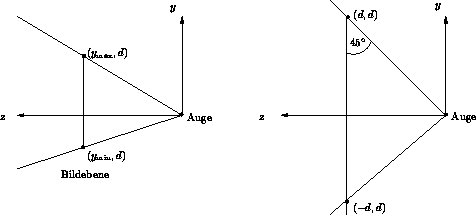
Es müssen also die y -Koordinaten proportional zur z -Koordinate
verändert werden.
Dies entspricht einer Scherung an der z -Achse und Skalierung, d.h.
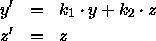
Punkt
(ymax,d ) soll abgebildet werden auf (d,d ) ;
Punkt
(ymin,d ) soll abgebildet werden auf (- d,d ) .
Durch Lösen des Gleichungssystems
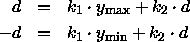
erhält man
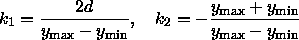
Analoge Scherung der x -Werte ergibt:
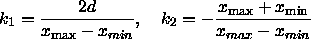
Als nächstes wird die regelmäßige Pyramide in den
Einheitswürfel
(0 x 1,0 y 1,0 z 1) transformiert.
Die front plane
entspricht der Ebene z = 0 und die
back plane
der Ebene z = 1 .
Da die y -Werte proportional zu den reziproken z -Werten skaliert werden müssen, ergibt sich als Transformation
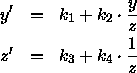
Der Kehrwert von z im Term zu z' ist erforderlich wegen der Verwendung von homogenen Koordinaten mit 4 × 4 -Transformationsmatrizen.
Punkt
(dmax,dmax) soll abgebildet werden auf (1,1) ,
Punkt
(- dmin,dmin) soll abgebildet werden auf (0,0) .
Durch Lösen des Gleichungssystems
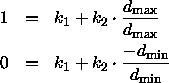
erhält man
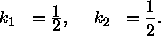
Durch Lösen des Gleichungssystems
erhält man
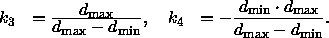
Die x -Werte werden analog zu den y -Werten skaliert. Insgesamt ergibt sich somit
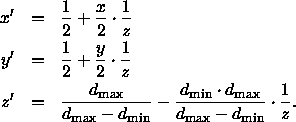
Zwar wird hierdurch die Szene im vorderen z -Bereich nicht-linear gestaucht, zur Bestimmung der Sichtbarkeit reichen die ermittelten z -Werte jedoch aus, da ihre Ordnung erhalten bleibt.
Durch Verknüpfen der beiden letzten Transformationen
erhält man in Schritt 3.) als Transformationsmatrix
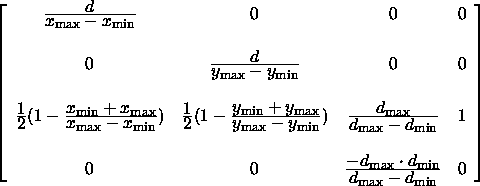
die den sichtbaren Teil der Szene in den Einheitswürfel transformiert.
Um wieder ein rechtshändiges Koordinatensystem zu erhalten, wird zunächst das Koordinatensystem so transformiert, daß die Back Plane in die xy -Ebene verschoben wird. Abschließend wird wieder an der xy -Ebene gespiegelt.
Für das Clippen von Kanten am Einheitswürfel bietet sich die dreidimensionale Erweiterung des Algorithmus von Cohen & Sutherland an: Der Bereichs-Code benötigt 6 Bits.