Bei den schiefen Parallelprojektionen stehen die Sehstrahlen
nicht normal auf der Bildebene,
sondern schneiden sie unter dem Winkel 
(Abbildung
14.5
).
Die schiefe Projektion auf die xy -Ebene
entspricht einer Scherung der x - und y -Koordinaten proportional
zu z .
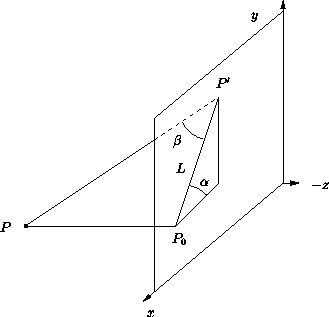
Seien
P0 = (x,y,0) die orthogonale und
P' = (x',y',0) die schiefe Projektion von Punkt P = (x,y,z) .
Sei L die Entfernung von P0 nach P' .
Dann gilt
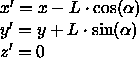
Wegen
tan() = 
folgt
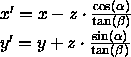
Der Winkel regelt im projizierten Bild das
Verhältnis von x -Ausdehnung zu z -Ausdehnung.
Die Koordinaten zweier projizierter Punkte
P'1 , P'2 lauten:
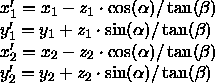
Für zwei Punkte, die sich nur bzgl. ihrer z -Koordinaten unterscheiden,
betragen die Abstände ihrer Bilder in x - bzw. y -Richtung
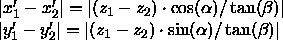
für den Abstand
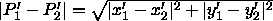
ergibt sich
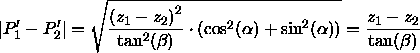
wegen
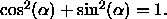
Für die Berechnung der Transformationsmatrix benötigt der Algorithmus
den Verkürzungsfaktor d und den Scherwinkel 
.
d gibt an,
um welchen Faktor zur Bildebene normal stehende Strecken verkürzt werden.
Es gilt
definiert den Winkel zur Horizontalen, unter dem diese Kanten
aufgetragen werden.
Für die Koordinaten des so projizierten Punktes
P = (x,y,z,1) gilt
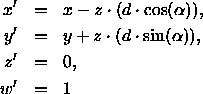
Die entsprechende Transformationsmatrix lautet
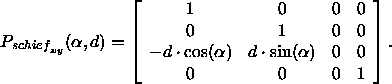
Für d = 0
(
= 90 o )
ergibt sich daraus die orthogonale Projektion.
Bei
schiefen Projektionen ist der Wert für d immer ungleich Null.
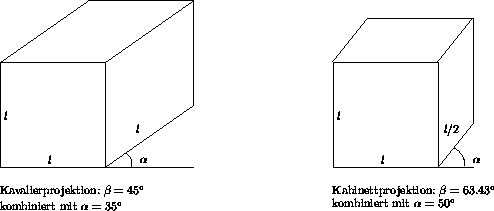
Zwei häufig als Ersatz für Perspektive verwendete Projektionen haben die
Werte d = 1 (
= 45 o ),
= 35 o (Kavalierprojektion) und
d = 0.5 (
= 63.43 o ),
= 50 o (Kabinettprojektion).
Bei der
Kavalierprojektion werden alle auf der Bildebene normal stehenden
Strecken unverkürzt abgebildet.
Bei der Kabinettprojektion
ergibt sich eine Verkürzung auf die Hälfte ihrer ursprünglichen Länge.
