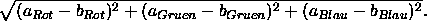
Optimaler Algorithmus
Gegeben sei eine Menge F von beobachteten Farben.
Gesucht ist eine Menge M von Repräsentanten, so daß der Ausdruck
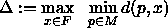
minimiert wird, d.h., 
ist der maximale Abstand, den eine Farbe zu ihrem
nächsten Repräsentanten hat.
Da die exakte Bestimmung von M eine exponentielle Laufzeit verursacht, begnügt man sich mit einer Näherungslösung.
Popularity-Algorithmus (1978)
Wähle die K häufigsten Farben.
Nachteil: Selten vorkommende Farben werden schlecht repräsentiert.
Diversity-Algorithmus ( xv , John Bradley, 1989)
Initialisiere M mit der häufigsten Farbe
for i := 2 to K do
erweitere M um die Farbe des Histogramms,
die zu allen Farben aus M den größten Abstand hat
end
Median-Cut (Heckbert, MIT 1980)
Initialisiere RGB-Wuerfel mit Häufigkeiten der beobachteten Farbtupel
Initialisiere Wurzel des Schnittbaums mit Gesamtzahl der Pixel
While noch_nicht_genügend_Blätter do
Wähle Blatt mit der größten Pixelzahl
Bestimme umschliessende Box
Bestimme Achse mit größtem Wertebereich
Durchlaufe Box längs dieser Achse
Teile am Median in zwei Hälften
Trage Hälften als Soehne ein
end
Für jedes Blatt wähle den Mittelwert aller in ihm liegenden Farben.
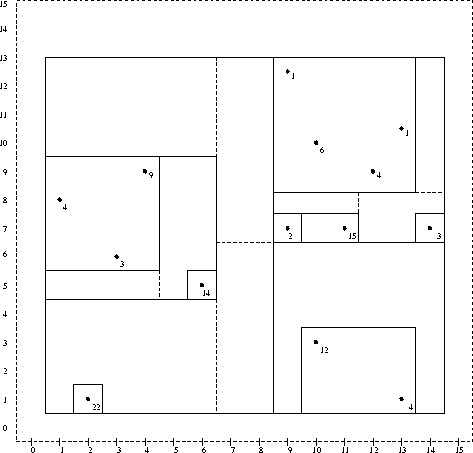
Abbildung 10.2 zeigt die Anwendung des Median-Cut-Algorithmus anhand eines Beispiels. Zur einfachen Darstellung ist der Farbbaum zweidimensional gewählt. Gezeigt wird die Verteilung der Farbtupel aus dem Bereich [0...15] × [0...15] in einem Bild mit 10 × 10 = 100 Pixeln. Eingetragen sind an der Position x/y die Häufigkeit des Farbtupels x,y . Schnittlinien sind gestrichelt, umschließende Boxen durchgezogen gezeichnet.
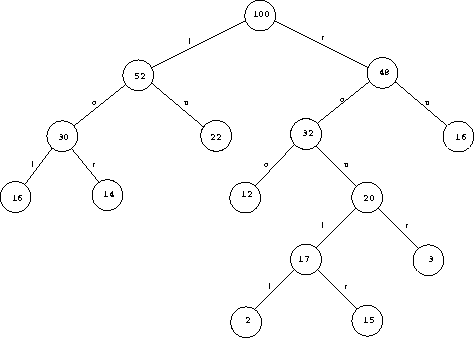
Abbildung 10.3 zeigt für das vorliegende Beispiel den Schnittbaum nach Anwendung des Median-Cut-Algorithmus. Die Knoten sind markiert mit der Anzahl der noch zu quantisierenden Pixel, an den Kanten ist vermerkt, ob es sich um einen Links/Rechts- oder um einen Oben/Unten-Schnitt handelt.
Floyd-Steinberg-Dithering (1975)
Der bei Verwendung einer Farbtabelle verursachte
Fehler beim Quantisieren eines Pixels wird auf die
Nachbarpixel verteilt (bevor diese quantisiert werden).
for (i = 0; i < M; i++)
for (j = 0; j < N; j++)
{
x = f[i][j]; /* hole Original-Farbe */
k = p(x); /* finde naechsten Repraesentant */
q[i][j] = k; /* zeichne quantisiertes Pixel */
e = d(x, k); /* bestimme Fehlerabstand */
f [i][j + 1] = f[i][j + 1] + e * 3.0/8.0;
f [i + 1][j] = f[i + 1][j] + e * 3.0/8.0;
f [i + 1][j + 1] = f[i + 1][j + 1] + e * 1.0/4.0;
}
16 Mill. Farben |
256 Farben |
16 Farben |
4 Farben |