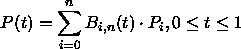
Der Punkt Pi wird gewichtet mit Hilfe eines Bernstein-Polynoms.
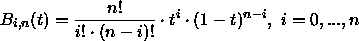
Beispiel: n = 3
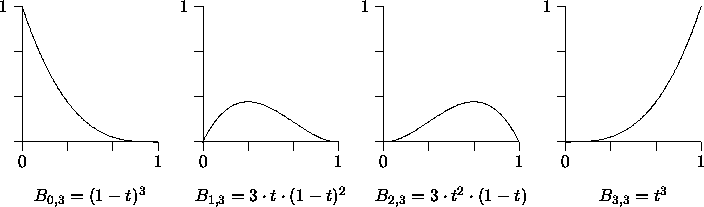
Die wichtigsten Eigenschaften der Bernsteinpolynome:
Da alle Bernsteinpolynome für 0 < t < 1 ungleich
Null sind, beeinflussen alle Stützpunkte in diesem Intervall den
Kurvenverlauf.
Die Kurve beginnt im Stützpunkt P0 tangential
zur Geraden
![]() , endet im Stützpunkt
Pn tangential zur Geraden
, endet im Stützpunkt
Pn tangential zur Geraden
![]() und verläuft innerhalb der konvexen Hülle der Stützpunkte.
Somit können mehrere Bézier-Kurven aneinandergesetzt werden
durch Identifikation von Endpunkt und Anfangspunkt aufeinanderfolgender
Bézierkurven.
Einen stetig differenzierbaren Übergang erreicht man bei Kollinearität
der Punkte
Pn - 1,Pn = Q0,Q1 .
und verläuft innerhalb der konvexen Hülle der Stützpunkte.
Somit können mehrere Bézier-Kurven aneinandergesetzt werden
durch Identifikation von Endpunkt und Anfangspunkt aufeinanderfolgender
Bézierkurven.
Einen stetig differenzierbaren Übergang erreicht man bei Kollinearität
der Punkte
Pn - 1,Pn = Q0,Q1 .
Berechnung der Bézier-Kurve nach de Casteljau
Es gilt:
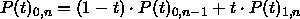
wobei die tiefgestellten Indizes angeben, welche Stützpunkte in die Berechnung einfließen. D.h. eine Bézier-Kurve vom Grad n läßt sich durch zwei Bézier-Kurven vom Grad n - 1 definieren, indem für ein festes t die Punkte beider Kurven berechnet werden, und die Verbindungsstrecke im Verhältnis t geteilt wird.
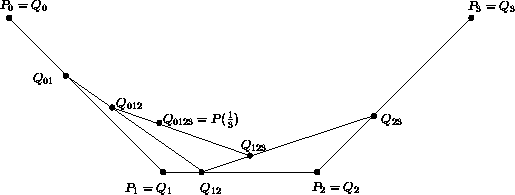
Berechnung eines Kurvenpunktes für
t = ![]() .
Die Indizes geben an, welche Stützpunkte beteiligt sind.
.
Die Indizes geben an, welche Stützpunkte beteiligt sind.
/****************************************************************************************/
/* */
/* Zeichnen einer Bezierkurve 3. Grades nach De Casteljau */
/* */
/****************************************************************************************/
private void bezier( // Zeichne eine Bezierkurve 3. Grades
double px0, double py0, // anhand des Stuetzpunktes p0
double px1, double py1, // anhand des Stuetzpunktes p1
double px2, double py2, // anhand des Stuetzpunktes p2
double px3, double py3, // anhand des Stuetzpunktes p3
int depth) // aktuelle Rekursionstiefe
{
double qx01,qy01,qx12,qy12,qx23,qy23,qx012,qy012,qx123,qy123,qx0123,qy0123;
// Hilfspunkte
if (depth > iter) // Iterationstiefe erreicht
set_line( new Point( (int)px0, (int)py0), new Point( (int)px3, (int)py3));
else {
depth++;
qx01 = (px0+px1)/2; qy01 = (py0+py1)/2;
qx12 = (px1+px2)/2; qy12 = (py1+py2)/2;
qx23 = (px2+px3)/2; qy23 = (py2+py3)/2;
qx012 = (qx01+qx12)/2; qy012 = (qy01+qy12)/2;
qx123 = (qx12+qx23)/2; qy123 = (qy12+qy23)/2;
qx0123 = (qx012+qx123)/2; qy0123 = (qy012+qy123)/2;
bezier (px0,py0,qx01,qy01,qx012,qy012,qx0123,qy0123,depth);
bezier (qx0123,qy0123,qx123,qy123,qx23,qy23,px3,py3,depth);
}
}
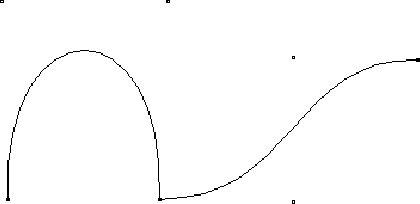
Vom De Casteljau-Algorithmus mit Rekursionstiefe 3 gezeichnete Bézierkurven