Die reellwertigen Koordinaten der Objekte im DC am Ende der Transformationspipeline müssen in ganzzahlige Pixelkoordinaten gerundet werden. Die Rasterung von Flächen kann mit Hilfe des Scanline-Verfahrens auf die von Linien zurückgeführt werden. In einem zweistufigen Algorithmus wird die Fläche zunächst in eine Menge horizontaler Linien, die sogenannten Spans, zerlegt. Die Eckpunkte dieser Spans ergeben sich durch Rasterung der Kanten nach dem vorgestellten Verfahren. In der zweiten Stufe wird dann jeder der Spans gerastert.
Das Scanline-Verfahren wird zur Vereinfachung und Beschleunigung des Rendering-Programms nur auf Dreiecke angewandt, denn Dreiecke sind die einfachsten Polygone. Gegenüber allgemeinen Polygonen bieten sie den Vorteil, daß sie planar und konvex sind. Für das Scanline-Verfahren eignen sie sich ausgezeichnet, da für jede Bildschirmzeile (Scanline) maximal zwei Schnittpunkte mit den Dreieckskanten auftreten.
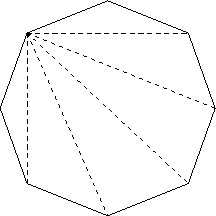
Ein konvexes Polygon läßt sich gemäß der Abbildung triangulisieren, indem von einem beliebigen Eckpunkt aus zu allen nicht benachbarten Eckpunkten Diagonalen gezogen werden.
Außerdem sind je nach Schattierungs-Verfahren auch die Farbwerte bzw. die Normalenvektoren, die in den Eckpunkten gegeben sind, über die Fläche zu interpolieren. Verschiedene Farbwerte auf den Objektflächen ergeben sich durch die individuelle Beleuchtung der Punkte. Die Interpolation der Normalen simuliert dabei einen gekrümmten Flächenverlauf. Grundlegend für die Schattierungs-Verfahren ist die Beleuchtung einer Szene mit Hilfe von unterschiedlichen Lichtmodellen.