



Es werden p Prozessoren verwendet, die jeweils
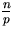 Zahlen speichern.
Zu Beginn sortiert jeder
Prozessor seine Liste in
O(
Zahlen speichern.
Zu Beginn sortiert jeder
Prozessor seine Liste in
O(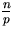 · log
· log 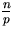 ) .
Als Pivotelement wird der Median genommen, der
bei einer sortierten Liste in konstanter Zeit
ermittelt werden kann.
Das Broadcasten
des Pivotelements dauert in der i -ten Phase
k - i + 1 Schritte.
Das Aufspalten der Liste
bzgl. des Pivotelements erfolgt in
O(log
) .
Als Pivotelement wird der Median genommen, der
bei einer sortierten Liste in konstanter Zeit
ermittelt werden kann.
Das Broadcasten
des Pivotelements dauert in der i -ten Phase
k - i + 1 Schritte.
Das Aufspalten der Liste
bzgl. des Pivotelements erfolgt in
O(log 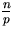 ) .
Der Transfer benötigt
O(
) .
Der Transfer benötigt
O(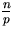 ) , das Mischen
ebenfalls
O(
) , das Mischen
ebenfalls
O(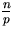 ) .
Also ergibt sich für die parallele Laufzeit
) .
Also ergibt sich für die parallele Laufzeit
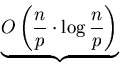 |
+ |
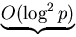 |
+ |
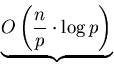 |
| lokales Sortieren |
|
Pivot Broadcast |
|
Split + Transfer + Merge |
Die Kosten betragen daher
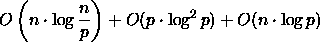
Für p 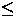 n ist der erste und letzte Term
O(n · log n) .
n ist der erste und letzte Term
O(n · log n) .
Für
p 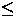 n/log n ist der zweite Term
O(n · log n) .
n/log n ist der zweite Term
O(n · log n) .
Also ist der Algorithmus für bis zu n/log n Prozessoren
kostenoptimal.




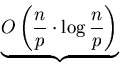
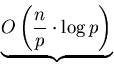
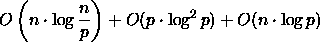
![]() n ist der erste und letzte Term
O(n · log n) .
n ist der erste und letzte Term
O(n · log n) .
![]() n/log n ist der zweite Term
O(n · log n) .
n/log n ist der zweite Term
O(n · log n) .