\section{Ein FEM-Verfahren}
\subsection{Methode der finiten Elemente}
FEM-Verfahren geh"oren zu den weitverbreitetsten numerischen L"osungsverfahren
f"ur Differentialgleichungen auf endlichen Gebieten. Das Berechnungsgebiet
wird dabei durch ein Netz von Zwischenpunkten in kleine Teilgebiete
zerlegt --- die finiten Elemente. Die L"osung der Differentialgleichung wird
jetzt elementweise approximiert, indem "uber jedem Element die Integralform
der DGl numerisch gel"ost wird. Dabei ist es n"otig, da"s der Wert
der L"osungsfunktion in den Netzpunkten bekannt ist. Da dies nicht der
Fall ist, wird hierf"ur ein angen"aherter Wert benutzt, der auf die gleiche
Weise berechnet wird. Es ergibt sich also eine Folge von N"aherungen in jedem
Netzpunkt. W"ahlt man eine geeignete Startl"osung, so kann bewiesen werden,
da"s diese Folge gegen die exakte L"osung konvergiert, falls die Netzdichte
klein genug ist. F"ur Punkte zwischen den Netzpunkten wird die L"osung
mit Hilfe des zugeh"origen Elements interpoliert.
F"ur die folgenden Betrachtungen gehen wir von einer einzelnen Funktion $f$
auf einem zweidimensionalen Gebiet aus. Diese Funktion wird mit Hilfe
sogenannter Ansatzfunktionen $N_i$ und der Funktionswerte an den Knoten $f_i$
approximiert:
\begin{equation}
f(x, y) = \sum_{i=1}^3 N_i f_i .
\end{equation}
Diese Ansatzfunktionen h"angen im wesentlichen von der Geometrie der finiten
Elemente ab. Wir verwenden bei zweidimensionalen Problemen nur lineare
Dreieckselemente, auf denen wir zur Bestimmung der $N_i$ ein spezielles
Koordinatensystem einf"uhren. Betrachten wir dazu ein solches Dreieck mit
den Koordinaten $(x_1, y_1), (x_2, y_2)$ und $(x_3, y_3)$ (Bild~2.1).
Wir f"uhren sogenannte Fl"achenkoordinaten $L_1, L_2$ und $L_3$ ein mit:
\begin{eqnarray}
x & = & L_1 x_1 + L_2 x_2 + L_3 x_3 \nonumber \\
y & = & L_1 y_1 + L_2 y_2 + L_3 y_3 \\
1 & = & L_1 + L_2 + L_3 . \nonumber
\end{eqnarray}



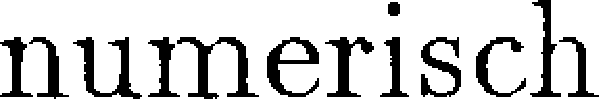
{\rtf0\pc{\fonttbl{\f0\fswiss Chicago;}
{\f2\froman New York;}{\f3\fswiss Geneva;}
{\f4\fmodern Monaco;}{\f5\fscript Venice;}
{\f6\fdecor London;}{\f7\fdecor Athens;}
{\f8\fdecor San Francisco;}
{\f11\fnil Cairo;}
{\f12\fnil Los Angeles;}
{\f20\froman Times;}
{\f21\fswiss Helvetica;}
{\f22\fmodern Courier;}{\f24\fnil Mobile;}}
{\stylesheet
{\s3\noline\plain \f20\fs36 \qj\sl000\li940\fi-940\tx940\f20 para3;}
{\s4\noline\plain \f20\fs36 \b\qj\sl000\li1040\fi-1040\tx1040\f20 para4;}
{\s5\noline\plain \f20\fs24 \qj\sl000\li0\fi0\f20 para5;}
{\s7\noline\plain \f20\fs24 \qc\sl000\li0\fi0\f20 cent7;}
{\s6\noline\plain \f20\fs24 \qj\sl000\li0\fi360\f20 para6;}
{\s8\noline\plain \f20\fs20 \qc\sl000\li0\fi0\f20 cent8;}
{\s1\noline\plain \f20\fs24 \ql\sl000\li0\fi0\ri0\keep\tx3000\tqdec\tx7760\f20 table1;}
{\s2\noline\plain \f20\fs20 \ql\sl000\li0\fi0\ri0\keep\tx2520\tx2880\tx3240\tqdec\tx7740\f20 table2;}
{\s3\noline\plain \f20\fs36 \qj\sl000\li940\fi-940\tx940\f20 para3;}
{\s4\noline\plain \f20\fs36 \b\qj\sl000\li1040\fi-1040\tx1040\f20 para4;}
{\s5\noline\plain \f20\fs24 \qj\sl000\li0\fi0\f20 para5;}
{\s7\noline\plain \f20\fs24 \qc\sl000\li0\fi0\f20 cent7;}
{\s6\noline\plain \f20\fs24 \qj\sl000\li0\fi360\f20 para6;}
{\s8\noline\plain \f20\fs20 \qc\sl000\li0\fi0\f20 cent8;}}
\sectd \cols1\endnhere \pard\plain \s3\noline\plain \f20\fs36 \qj\sl000\li940\fi-940\tx940\f20
{\plain \f20\fs36 2.2\tab Ein F`EM-Verfahren}
\par \par \pard\plain \s4\noline\plain \f20\fs36 \b\qj\sl000\li1040\fi-1040\tx1040\f20
{\plain \f20\fs36 \b 2.2.1\tab Methode der finiten Elemente}
\par \pard\plain \s5\noline\plain \f20\fs24 \qj\sl000\li0\fi0\f20
{\plain \f20\fs24 FEM-Verfahren gehören zu d
en weitverbreitet sten nun~erischen Lösungsverfahren für D ifferent i alglei d~ung
en auf endli den Gebieten. Das ß erechnungsgebiet wird dabei durch ein Netz von
Zwisd~enpunkten in kleine Teilgebiete zerlegt die finiten Elen~ente. Die Lösung der
Differentialgleid~ung wird jetzt eIen~entweise approxiu~iert, inden~ über jeden- Ele
n~ent die Integralforn~ der DGI nui~erisd~ gelöst wird. Dabei ist es nötig, dat der
Wert der Lösungsfunktion in den Netzpunkten bekannt ist. Da dies nicht der Fall i
st, wird hierfür ein angenäherter Wert benutzt, der auf die gleid~e Weise berechue
t wird. Bs ergibt sid~ also eine Folge von Näherungen in jeden- Netzpunkt. Wählt i
exakte Lösung konvergiert, falls die Netzdid~te klein genug ist. Für Punkte zwisc
hen den Netzpunkten wird die Lösung i~it liilfe des zugehörigen Elen~ents interpoli
ert.}\par \pard\plain \s6\noline\plain \f20\fs24 \qj\sl000\li0\fi360\f20
{\plain \f20\fs24 Für die folgenden Betradftungen gehen wir von einer einzelnen Funktion f auf
einen- zweidin~ensionalen Gebiet ans. Diese Funktion wird n~it llilfe sogenannter A
nsatzfunktionen N~ und der Funktionswerte an den Nnoten ft approxin~iert:}
\par \pard\plain \s7\noline\plain \f20\fs24 \qc\sl000\li0\fi0\f20
{\plain \f20\fs24 3}\par \pard\plain \s1\noline\plain \f20\fs24 \ql\sl000\li0\fi0\ri0\keep\tx3000\tqdec\tx7760\f20
\tab {\plain \f20\fs24 f(x,y) }{\plain \f20\fs20 =\tab }{\plain \f20\fs24 (
2.1)}\par \pard\plain \s7\noline\plain \f20\fs24 \qc\sl000\li0\fi0\f20
{\plain \f20\fs24 i=I}\par \par \pard\plain \s6\noline\plain \f20\fs24 \qj\sl000\li0\fi360\f20
{\plain \f20\fs24 Diese Ansatzfunktionen hängen ins wesentlichen von der Geon~etrie der finit
en Elen~ente ab. Wir verwenden bei zweidin~ensionalen Problen~en nur lineare Dreied~s
elen~ente, auf denen wir zur Bestin~n~ung der N~ ein spezielles l~oordinatensysten~ ein
führen. Betradften wir dazu ein sold~es Dreieck n~it den Noordinaten (x}{\dn6 1}{, yi), (x}{\dn6 2}{,
Y2) und (x}{\dn6 3}{, y~) (Bild 2.1).}\par \pard\plain \s6\noline\plain \f20\fs24 \qj\sl000\li0\fi360\f20
{\plain \f20\fs24 Wir führen sogenannte Flächenkoordinaten L}{\dn6 1}{, L}{\dn6 2 }{und L}{\dn6 3 }{ein n~it:}
\par \par \par \pard\plain \s2\noline\plain \f20\fs20 \ql\sl000\li0\fi0\ri0
\keep\tx2520\tx2880\tx3240\tqdec\tx7740\f20 \tab {\plain \f20\fs24 x\tab }
{\plain \f20\fs20 =\tab L}{\dn6 1}{x}{\dn6 1 }{+ L}{\dn6 2}{x}{\dn6 2 }{+ L}{\dn6 3}{x}{\dn6 3}
{\line \tab y\tab =\tab L}{\dn6 1}{y}{\dn6 1 }{+ L}{\dn6 2}{y}{\dn6 2 }{+ L}{\dn6 3}{y}{\dn6 3\tab }
{(2.2)\line \tab \tab =\tab L}{\dn6 1}{+L}{\dn6 2}{+L}{\dn6 3}{.}
\par \par \par \par \par \pard\plain \s8\noline\plain \f20\fs20 \qc\sl000\li0\fi0\f20
{\plain \f20\fs20 42}}

korrespondierende Ausschnitte
ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff ff
81 ff
aus dem Hex-Dump zu diss.tifll (Run Length Encoding)
($81 ff = 257-129 mal Weiß)
Speicherbedarf der am Einscannen beteiligten Dateien:
File
Bytes
%
Inhalt
diss.tex
2.073
0.1
Quelle im tex-Format
diss.ps
32.657
1.8
durch Quelle erzeugte Postscript-Datei
diss.tif
1.947.078
100.0
vom Scanner erzeugte TIF-Datei
(400 dpi => 3328 x 4680 Pixel)
diss.tifll
306.924
15.8
komprimiert mit Run Length Encoding
diss.tif5
153.126
7.8
komprimiert mit LZW
diss.tif3
127.932
6.5
komprimiert mit CCITT Group T4
diss.rtf
4.481
0.2
von OCR-Software erzeugte RTF-Datei