Datenstruktur: Keller (Aufwand bei vollbesetztem Graph: O(n!) )
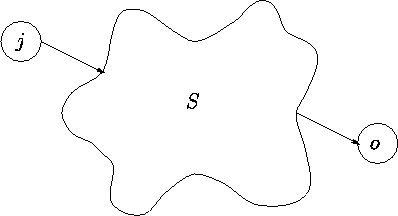
g(i, ![]() ) : = c(i,o)
) : = c(i,o)
g(i,S) : = ![]() {g(j,S
{g(j,S![]() {j}) + c(i,j)},(i
{j}) + c(i,j)},(i![]() S)
S)
Lösung des TSP:
g(o,V![]() {o})
{o})
Platzbedarf (Speicher):
![]()
Laufzeit: O(2n) (gute Verbesserung gegenüber O(n!) )
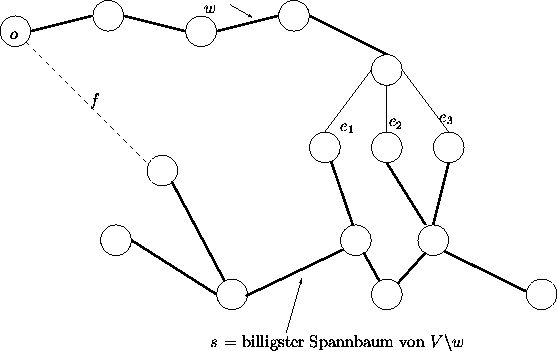
Eine Schranke bi für Ti lautet:
c(w) + c(ei) + c(S) + c(f )
( f = billigste Kante von
V![]() w zum Knoten o ).
w zum Knoten o ).
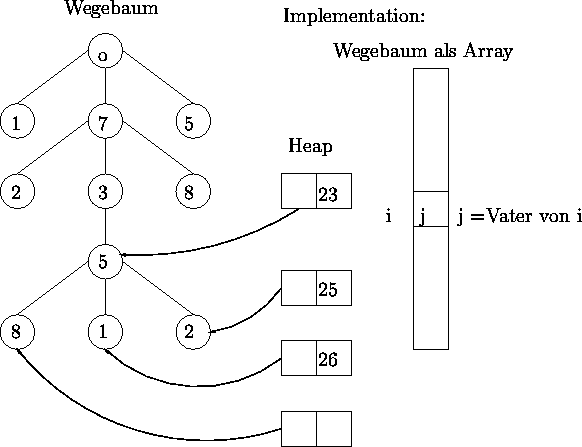
Algorithmus:
Startproblem <o, 0 > in Heap.
Sei L0 eine Näherungslösung.
REPEAT
Entferne billigste Teillösung T = <w,b > aus Heap.
Expandiere w zu w1 , w2 , ... , wk mit b1 , b2 , ... , bk .
Falls Lösung entsteht und besser als L0 , dann ersetzen.
Sinnvolle Teilprobleme in den Heap tun.
UNTIL Heap enthält keine sinnvollen Probleme mehr.
L0 ist Lösung.
(Teil-) Problem sinnvoll ![]() b -Wert < bisher beste Lösung ( L0 ).
b -Wert < bisher beste Lösung ( L0 ).
Laufzeit: exponentiell (z.B. O((1,2)n) )