9.1 Erweiternder Kreis

Ein erweiternder Kreis bzgl. eines Flusses f ist ein erweiternder Weg von einem Knoten x zu sich selbst.

Beispiel:

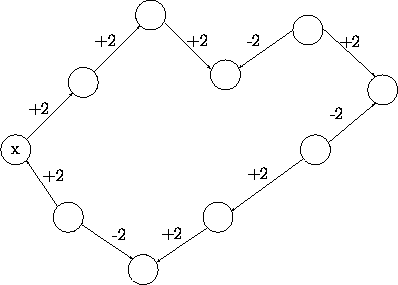
Offenbar läßt sich längs eines erweiternden Kreises ein Fluß umlenken, ohne seine Mächtigkeit zu verändern.

Daraus ergibt sich der folgende Satz: Fluß f hat minimale Kosten $\iff$ Es gibt bzgl. f keinen kostenmindernden erweitern den Kreis.

Konstruiere also aus f und G einen Graphen G_f = (V,E_f) mit folgenden Kantenkosten:

Beispiel:

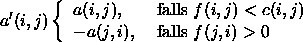
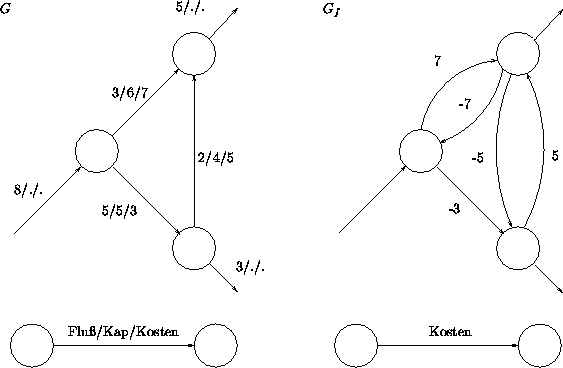
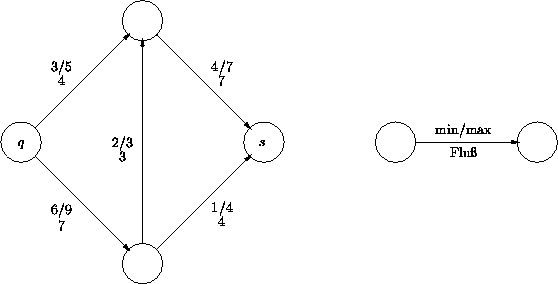
Ein kostensenkender Kreis in G entspricht einem Kreis negativer Länge in G_f . Im obigen Beispiel haben wir z.B. in G_f einen Kreis der Länge -1. Ändere nun den Fluß um das Minimum der Möglichkeiten, in unserem Fall also um min {3,2,5} = 2 . Die Ersparnis beträgt dann also: - 2 · 7 + 2 · 5 + 2 · 3 = 2 . Zur Erkennung von negativen Zyklen in G_f kann man z.B. den Algorithmus von Floyd verwenden, denn wenn im Laufe dieses Algorithmus in der Hauptdiagonalen der Entfernungsmatrix ein negativer Wert auftaucht, so liegt ein negativer Zyklus vor.

Gegeben: G = (V,E) gerichtet mit oberen und unteren Schranken:

$$\begin{array} {l} o: E \to \mathbb {Z} (\textrm{ob. Schr.})\ u: E \to \mathbb {Z} (\textrm{unt. Schr.})\end{array}$$

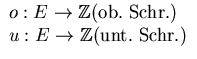
Gesucht: Ein zulässiger Fluß in G , d.h. ein Fluß, der die Schranken respektiert.

Beispiel:

Um dieses Problem zu lösen, betrachten wir einen modifizierten Graphen G' = (V',E') mit V' = V $\cup$ {q',s'} und E' = E $\cup$ {q'} × V $\cup$ V × {s'} $\cup$ {(q,s),(s,q)} .

Den Kanten aus E' ordnen wir dabei Kapazitäten zu, und zwar:

• $\forall$x,y $\in$ V : c(x,s') : = Summe der Mindestflüsse aus x heraus
• $\forall$x $\in$ V : c(q',x) : = Summe der Mindestflüsse aus x hinein
• $\forall$x,y $\in$ V,x $\neq$ y : c(x,y) : = o(x,y) - u(x,y)
• c(q,s) = c(s,q) : = $\infty$

Es ergibt sich in unserem Beispiel folgender Graph G' :

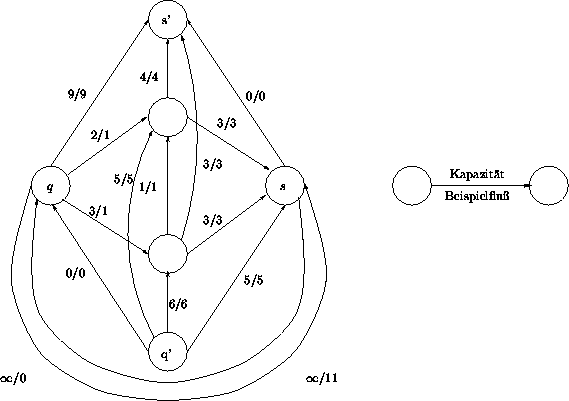
In diesem Graphen G' suchen wir nun den maximalen Fluß von q' nach s' . Ein solcher Fluß ist in dem obigen Schaubild eingezeichnet.

Für diesen Fluß gilt dann der folgende Satz:

G' hat einen Fluß f' der Größe S$\iff$G hat einen zulässigen Fluß f

(wobei S : = Summe der Mindestreinflüsse in s' = Summe der Mindestrausflüsse aus q' ). Somit können wir jetzt also entscheiden, ob G einen zulässigen Fluß besitzt oder nicht. Aber wie können wir diesen zulässigen Fluß f aus f' berechnen? Die Antwort gibt folgende Formel:

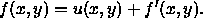
Die Idee dieses Verfahrens sei nun noch einmal zusammengefaßt:

Die ausgelasteten Zusatzkanten von q' bzw. nach s' erzwingen in jedem Knoten ein ``Flußgefälle'', welches durch die ursprünglichen Mindestflüsse diktiert wurde und welches durch die Restkapazitäten kompensiert wird.