8.4 Cut

Ein Cut des Graphen G = (V,E) ist eine Partition der Knotenmenge V in S und S' , so daß gilt: s $\in$ S und t $\in$ V$\backslash$S = $\overline{S}$ . Sei dann (S,$\overline{S}$) : = {(x,y) $\in$ E|x $\in$ S,y $\in$ $\overline{S}$} . Die Kapazität eines Cuts ist dann festgelegt durch c(S) : = $\sum\limits_{e\in(S,\overline{S})}^{}$c(e) .

Daraus folgt unmittelbar der folgende Satz:

Sei f ein Fluß der Größe F , sei S ein Cut von G

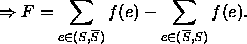
Der Fluß ist also an jedem beliebigen Cut meßbar.

Aus diesem Satz folgt aber direkt:

Sei f ein Fluß der Größe F , sei S ein Cut von G

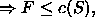
d.h. der Fluß ist höchstens so hoch wie die Kapazität eines Cuts.

$\Rightarrow$

Ist ein Fluß f so groß wie die Kapazität eines Cuts S , so ist f ein maximaler Fluß und S ist ein minimaler Cut bezogen auf seine Kapazität c(S).

Betrachte nun also folgende Situation:

Es gibt in G keine erweiternden Wege mehr. Dann enden also alle von s ausgehenden erweiternden Wege - genauer gesagt deren Anfangsstücke - entweder bei einer saturierten Vorwärtskante oder bei einer Rückwärtskante mit Fluß 0. Durch diese Kanten wird also ein Cut S impliziert, dessen Kapazität gleich dem momentanen Fluß ist. Daher muß der momentane Fluß aufgrund des letzten Satzes maximal sein. Somit ist der fehlende Beweis von vorhin erbracht.

Der Algorithmus kann also so notiert werden:

     Sei f = 0 der initiale Fluß
     REPEAT
          Suche bzgl. f einen erweiternden Weg von s nach t
          falls gefunden: erhöhe f längs dieses Weges.
     UNTIL kein erweiternder Weg gefunden
     Der Fluß f ist nun maximal.

Die Idee für die Suche nach einem erweiternden Weg in G ist eine Breitensuche in G , die beim Knoten s beginnt:

     Markiere s;
     WHILE möglich AND t ist nicht markiert DO
          Sei x ein markierter Knoten;
          IF $\exists$ unmarkiertes y mit (x,y) $\in$ E und f(x,y)<c(x,y) THEN
               markiere y und vermerke seinen Vorgänger x;
               $\delta$ (x,y) := c(x,y) - f(x,y);
          IF $\exists$ unmarkiertes y mit (y,x) $\in$ E und f(y,x) > 0 THEN
               markiere y und vermerke seinen Vorgänger x;
               $\delta$ (x,y) := f(y,x);
     END;

Eine interessante Eigenschaft von Netzwerken mit ganzzahligen Kapazitäten ist, daß auch die maximalen Flüsse in solchen Netzwerken immer ganzzahlig sind, da der obige Algorithmus nur ganzzahlige Erhöhungen durchführt.

Anmerkung: Bei irrationalen Kantenkapazitäten konvergiert der Algorithmus nicht zwingend. Solche Anwendungen sind in der Praxis aber auch sehr selten zu finden und daher ist diese Eigenschaft nicht von großer Bedeutung.

Betrachten wir nun das Laufzeitverhalten des Algorithmus anhand eines Beispiels:

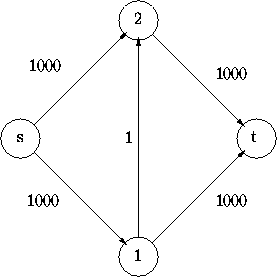
Bei ungeschickter Wahl des ersten erweiternden Weges, nämlich s,1,2,t , ist in der ersten Iteration lediglich eine Erhöhung um eine Einheit möglich. Wir saturieren also lediglich die Kante (1,2) . Als nächsten erweiternden Weg können wir nun s,2,1,t wählen, wobei auch hier wieder nur eine Erhöhung um eine Einheit zu erreichen ist. Wiederholt man diese beiden Wahlen immer wieder, so benötigt man insgesamt 2000 (!) Iterationen, bis man den maximalen Fluß gefunden hat.

Die Laufzeit liegt also im worst case in O(|E| · v) , wobei v der maximale Fluß in G ist. Der Algorithmus hat also ein exponentielles Laufzeitverhalten relativ zur Darstellungslänge des Graphen in einem Rechner.

Im weiteren werden wir uns nun damit beschäftigen, wie wir durch geschicktere Wahl der erweiternden Wege die Komplexität des Algorithmus erheblich verbessern können.

Dafür gibt es im wesentlichen zwei Ansätze:

1.

Finde jeweils den erweiternden Weg mit der größtmöglichen Erhöhung.

2.

Finde jeweils den kürzesten erweiternden Weg.

Im ersten Fall erreichen wir damit eine Verbesserung der Laufzeit auf O(|E| · log v) , in zweiten Ansatz erreichen wir eine Komplexität von O(|V|³ · |E|) , also eine Komplexität, die vollkommen unabhängig vom maximalen Fluß in G ist.

Es existiert eine große Anzahl von Anwendungsmöglichkeiten für Max-Fluß-Probleme, von denen hier einige näher vorgestellt werden sollen:

Gegeben: G = (V,E) gerichtet, s , t $\in$ V seien die Quelle bzw. Senke von G .

Frage: Wieviel knotendisjunkte Wege gibt es von s nach t ?

Um diese Frage zu beantworten, modifiziert man das vorliegende Netzwerk, indem man jeden Knoten x durch zwei Knoten x₁ und x₂ ersetzt, die mit einer Kante mit Kapazität 1 verbunden werden:

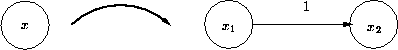
Außerdem ersetzt man jede Kante (x,y) durch die neue Kante (x₂,y₁) :

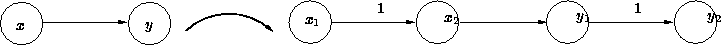
Nun bestimmt man mit den bekannten Algorithmen den maximalen Fluß in diesem modifizierten Netzwerk. Dessen Größe entspricht dann offensichtlich der Anzahl der knotendisjunkten Wege von s nach t .