3.2 2-fach zusammenhängend

Ein Graph heißt 2-fach zusammenhängend, wenn er nur aus einem Knoten besteht oder (für |V| > 2 ) wenn er keine Artikulationspunkte hat.

In einem 2-fach zusammenhängenden Graphen ist jedes Knotenpaar durch mindestens zwei kanten- und knotendisjunkte Wege verbunden.

Ein nicht 2-fach zusammenhängender Graph zerfällt in 2-fach Zusammenhangskomponenten, das sind die maximalen 2-fach zusammenhängenden Teilgraphen (siehe Umrahmungen oben).

Ergebnis einer Tiefensuche:

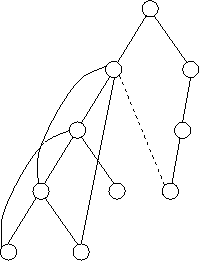
Die dünnen Kanten stellen ``Rückwärtskanten'' dar, d.h. Kanten, über die zurückgesprungen wird, wenn der Algorithmus in eine Sackgasse gelaufen ist. Solche Kanten wie die gestrichelte Kante sind im Ausgangsgraphen nicht möglich!

Für jede Kante (x,y) gilt: x ist Vorfahre von y oder y ist Vorfahre von x .

Behauptung:

Die Wurzel ist Artikulationspunkt $\iff$ Sie hat 2 oder mehrere Söhne.

Beweis:

$$\Rightarrow$$ Die Wurzel ist Artikulationspunkt.

$$\Rightarrow \ge$$

$$\Rightarrow$$

$$\Leftarrow$$ Die Wurzel hat 2 oder mehrere Söhne.

$$\Rightarrow$$

$$\Rightarrow$$

$$\Rightarrow$$

Behauptung:

Ein Knoten k $\neq$ Wurzel ist Artikulationspunkt

$\iff$ Es gibt einen Sohn x von k , der nicht von sich oder seinen Nachfahren einen Vorfahren von k erreichen kann.

Beweis:

$$\Rightarrow$$ k sei ein Artikulationspunkt. Annahme: Alle Söhne von k erreichen einen Vorfahren von k .

$$\Rightarrow$$

$$\Rightarrow$$

$$\Leftarrow$$ Von x gehe keine Kante zu einem Vorfahren von k .

$$\Rightarrow$$

$$\Rightarrow$$

$$\Rightarrow$$

Aus diesen Eigenschaften läßt sich demzufolge ein Verfahren zur Ermittlung der Artikulationseigenschaft eines jeden Knotens ableiten:

Berechne während der Tiefensuche für jeden Knoten k den höchsten Knoten, den seine Söhne mit Rückkanten erreichen können. Dadurch kann man entscheiden, ob k ein Artikulationspunkt ist oder nicht.

Es folgt der Algorithmus, der diesen höchsten erreichbaren Knoten berechnet:

PROCEDURE visit (k: INTEGER): INTEGER;
BEGIN
id := id + 1; val[k] := id; besucht[k] := TRUE; min := val[k];
reset(g[k]);
WHILE NOT endpos(g[k]) DO
     x := elem(g[k]);
     IF NOT besucht[x] THEN m:= visit(x);
          IF m < min THEN min := m;
          IF m $\geq$ val[k] THEN Write(4k ist Artikulationspunkt.4); END
     ELSE (* Rückkante *)
          IF val[x] < min THEN min := val[x]; END;
     END;
     advance(g[k]);
END (* WHILE *)
RETURN min;
END (* visit *)

Dies ist also ein Beispiel dafür, wie man eine Tiefensuche sinnvoll nutzen kann!