1.1 Modellierungsmöglichkeiten von Graphen

Der Graph wird als 2-Tupel, bestehend aus der Knotenmenge V und der Kantenmenge E , definiert:

G = (V,E)

Die Knoten symbolisieren hierbei die jeweiligen Objekte, und die Kanten modellieren binäre Beziehungen zwischen diesen Objekten.

Man unterscheidet nun zwischen gerichteten und ungerichteten Graphen. Im gerichteten Fall ist die Kantenmenge E eine Teilmenge des kartesischen Produkts der Knotenmenge mit sich selbst: E $\subseteq$ V × V . Eine Kante ist also ein gerichtetes Paar, man schreibt (x,y) $\in$ E .

Im ungerichteten Fall ist E eine Teilmenge von P ₂(V) (Menge aller 2-elementigen Teilmengen von V ): E $\subseteq$ P ₂(V) . Eine Kante ist dann also eine 2-elementige Teilmenge von V : {x,y} $\in$ E . Häufig schreibt man aber -- wie im gerichteten Fall -- (x,y) $\in$ E (und somit auch (y,x) $\in$ E ).

In gegebenen Fällen werden die Kanten des Graphen noch zusätzlich mit einer Gewichtung c : E$\to$$\mathbb {R}$ versehen, die z.B. Kosten einer Verbindung modellieren.

Beispiele:

Aufgabe:

Gegeben: 3 Wassereimer à 7 Liter (voll), 3 Liter und 1 Liter (beide leer).

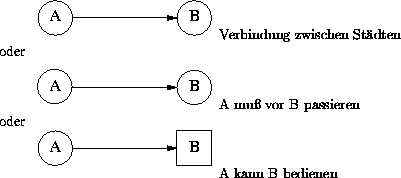
Gesucht: Folge von Umfüllaktionen, die letztendlich in einem Eimer 5 Liter abmessen.

Modell:

Knoten entsprechen Zuständen, z.B. Start mit (7,0,0) .

Kanten werden für Umfüllaktionen eingeführt, z.B. (7,0,0)$\to$(4,3,0) .

Evtl. können die Kanten noch mit dem Eimergewicht des umgefüllten Eimers als Gewichtung versehen werden.

Eine Lösung des Problems ist jetzt gleichzusetzen mit einem Weg in dem beschriebenen Graphen von (7,0,0) nach (5, · , · ) .

Für diesen Weg sind nun -- neben der Existenz eines solchen Weges -- evtl. verschiedene Optimalitätsbedingungen wichtig:

• Man sucht einen Weg mit möglichst wenigen Umfüllaktionen, also einen Pfad in G mit möglichst wenig Kanten.
• Man sucht einen ``kraftsparenden'' Weg in G , d.h. einen Pfad mit möglichst geringer Summe der o.a. Kantenkosten.

Aufgabe:

Straßenkreuzung mit verschiedenen Abbiegemöglichkeiten

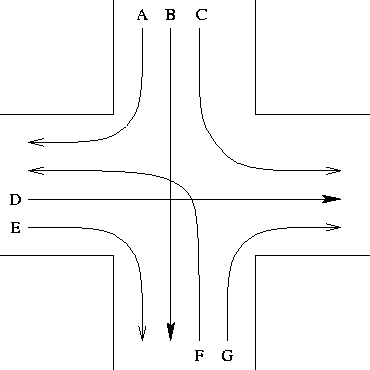
Dieses Problem modellieren wir nun durch einen ungerichteten Graphen, dessen Knoten die verschiedenen Abbiegemöglichkeiten (A - G) und dessen Kanten evtl. Konflikte zwischen zwei Möglichkeiten simulieren. Wir erhalten also folgenden (ungerichteten) Graphen:

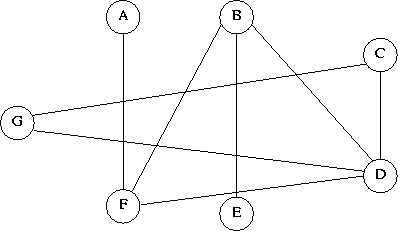
Als Problem gilt es jetzt, die Anzahl der Ampelphasen zu minimieren. Dies ist gleichbedeutend mit dem Problem, im obigen Graphen eine Färbung der Knoten mit minimaler Farbzahl zu finden. Bei der Einfärbung der Knoten muß man dabei beachten, daß benachbarte Knoten unterschiedliche Farben haben müssen.