10.2 Bipartiter Graph

Am häufigsten werden Matchingprobleme in bipartiten Graphen betrachtet. Das sind Graphen G = (V,E) , für die gilt: V = V₁ $\cup$ V₂ (disjunkt) und E $\subseteq$ V₁ × V₂ . Wir wollen uns daher in den nächsten Ausführungen zunächst auf solche Graphen konzentrieren.

Die Frage ist nun, wie man in bipartiten Graphen ein Maximum Matching bestimmen kann. In diesem ersten Ansatz lösen wir dieses Problem unter Mithilfe von Flußalgorithmen, genauer gesagt mit der Berechnung von maximalen Flüssen:

Transformiere den Graphen G = (V,E) in ein gerichtetes Netzwerk G' = (V',E') mit V' = V $\cup$ {s,t} und E' = E $\cup$ {(s,x)|x $\in$ V₁} $\cup$ {(y,t)|y $\in$ V₂} . Die Kanten aus E werden in G' als gerichtet betrachtet und zwar von V₁ nach V₂ . Den Kanten von s aus und nach t hinein wird die Kapazität 1 zugeordnet.

Beispiel:

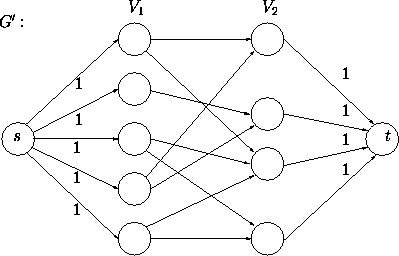
Durch die Kapazitäten der (s,.) - und (.,t) -Kanten wird die Unabhängigkeit der Kantenmenge erreicht, die unser Matching darstellen soll. Führt man nämlich in G' eine Max-Fluß-Betrachtung durch, so entspricht ein Fluß der Größe k in G' einem Matching M der Kardinalität k .

Sei M nun ein Matching in G = (V,E) .

Ein Knoten v heißt belegt, wenn er von einer Matchingkante berührt wird. Ist dies nicht der Fall, so heißt er frei.