Today usually the logarithm with base 2 is chosen and the resulting
information-units are called binary digits, or bits. Therefore one relay or flip-flop which
can be in any of two stable positions holds 1 bit of information. N such
devices can store N bits, since the total number of possible states is 2Nand
![]() (adapted from [40]):
(adapted from [40]):
| (4) |
To evaluate the information content of knowing a current state ![]() we
compare the a priori information (set Sn) with the a posteriori information
(set
we
compare the a priori information (set Sn) with the a posteriori information
(set ![]() ). In general our a posteriori information can be in any
subset
). In general our a posteriori information can be in any
subset
![]() .
Our knowledge about a particular
subset U or state
.
Our knowledge about a particular
subset U or state ![]() is expressed by the conditional Hartley information
is expressed by the conditional Hartley information
![]() :
:
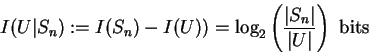 |
(5) |
Note that the information we have (in bits) if we know the state can be interpreted as the uncertainty (in bits) if we don't know the state. In the above example our uncertainty is N bits if we don't know the states of N (binary) relays, and thus we are uncertain about N bits of information.
Sometimes the set of states is partitioned into clusters. Let Ck be a partion of
Sn:
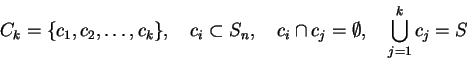
The relative information is also used to evaluate the (statistical)
significance of distributions. Here the single data entries are the states and their
respective variable values are the corresponding clusters.
Example, if there are 400 data entries
![]() ,
200 with value
,
200 with value ![]() ,
and
also 200 with value v1 in V then
I(V|D)=log(2)/log(400)=0.1157.
If there are only two data entries
,
and
also 200 with value v1 in V then
I(V|D)=log(2)/log(400)=0.1157.
If there are only two data entries
![]() ,
one with value v1 and one with v2then
I(V|D)=log(2)/log(2)=1, which is the highest amount of possible relative information
for a partition. We know that estimated probabilities of
,
one with value v1 and one with v2then
I(V|D)=log(2)/log(2)=1, which is the highest amount of possible relative information
for a partition. We know that estimated probabilities of
![]() are much more significant for the first case then for the second.
Therefore a lower relative information among the values indicate higher
significance for a probability approximation.
are much more significant for the first case then for the second.
Therefore a lower relative information among the values indicate higher
significance for a probability approximation.