As an formal example assume a table R, here also called relation, of cars:
| s (No.) | x1 (car-type) | x2 (color) |
| 1 | Ford | black |
| 2 | Dodge | red |
| 3 | Ford | white |
| 4 | Ford | black |
| 5 | Chevy | blue |
| 6 | Dodge | red |
| 7 | Dodge | red |
The relation R can be also described by its characteristic
function ![]() over support S and variables X1,X2:
over support S and variables X1,X2:
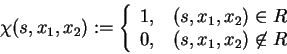 |
(1) |
 |
(2) |
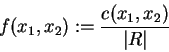 |
(3) |
| x1 (type) | x2 (color) | c(x1,x2) (count) | f(x1,x2) (probability) |
| Ford | black | 2 | 2/7 |
| Dodge | red | 3 | 3/7 |
| Ford | white | 1 | 1/7 |
| Chevy | blue | 1 | 1/7 |
| total | 7 | 1 |
Can we have structure in a single dimension? Definitively not if the values in that dimension are randomly distributed. That random distribution would tell us something about this dimension (i.e. that there is no structure) but would leave us with an unstructured mess of values. Thus we associate some structure with a variable if its value-distribution allows some predictability; that is if the value-distribution is different from a random distribution. As an example, imagine a distribution where 50% of the cars are red and 50% are black. If red and black are the only values for car colors then this dimension is randomly distributed and doesn't give us any information for prediction. If 90% of the cars are red and only 10% are black the situation is entirely different. We can find the ``structure'' that red cars are much more likely to appear than black ones. ``Structure'' seems to be connected with the distribution of the variable-values. You can compare this with fitting a distribution (Normal, Exponential, Gamma,..) in the continuous case.
Going to two or more dimensions, the relationships between variables are involved. We think of high structure if specific values of one variable mostly appear together with a specific value of another variable. In statistical terms, we say the variables are ``correlated''; however, statistical correlation does not work for nominal variables (neither mean, variance, nor covariance are defined on a nominal probability space). Looking to the joint-distribution of the variables we see that this ``appearing together'' again just means a ``structured'' distribution of values instead of a random distribution. The probability for some value-tuples is pretty high (for those values which mostly appear together) while other probabilities remain small.
This becomes even more clear if we reduce the distribution again to a one- dimensional case by looking at the conditional distribution f(Y | X=x). We fix one value in dimension X and look how the values of Y distribute in this case (see Section 2.3.2 ). If the resulting distribution is random, then our chosen value in X seems not related to the dimension Y. But if the value x mostly occurs with one value in Y the conditional distribution will be highly structured and the predictive uncertainty low.
When we look for some kind of pattern we often have some entities which have something in common (on which we conditionalize). We want to figure out what else they have in common (what structure there might be in the conditional distribution). Consider this example from programming. In some cases a program returns an error (in the space of program-runs this is the first thing the have in common). The programmer then wants to know what else these runs have in common so he can find out what could have triggered the error. If all these runs show a specific and distinct pattern in the input-values then the problem might be connected with these inputs.
In this sense the structure within a dataset can be measured by the randomness or uncertainty of its value-distribution (or conditional distribution, etc.)