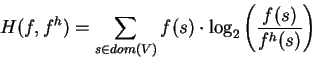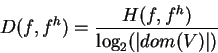


Next: Search through Model-Space:
Up: Reconstructability Analysis (RA)
Previous: Join-procedure:
If
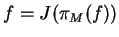 ,
then f is called ``reconstructable'' from our model M. We can represent
the data without information loss by using model M and the assumptions made about
independencies seem to be correct.
A distribution f is regarded as ``approximately reconstructable'' from a model M if
the maximum entropy reconstruction
,
then f is called ``reconstructable'' from our model M. We can represent
the data without information loss by using model M and the assumptions made about
independencies seem to be correct.
A distribution f is regarded as ``approximately reconstructable'' from a model M if
the maximum entropy reconstruction
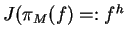 is sufficiently `close' to f
according to some distance-measure.
is sufficiently `close' to f
according to some distance-measure.
A well known class of distance-measures is the Minkowski-class of distances
(parameterized by
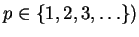 ,
also known as L-norms:
,
also known as L-norms:
which contain the Hamming-distance (L1), the Euclidean-distance (L2), and the
Max-distance (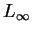 ).
).
For measuring the accuracy of the model we are more interested in the information loss
of the maximum entropy reconstruction compared to the original distribution.
The following two non-symmetric measures are derived from information-theory:
Shannon's cross-entropy, also known as directed divergence
[28, pg. 279], [38, pg. 12]:
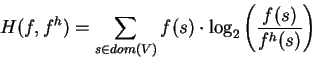 |
(21) |
and the relative information loss by normalizing Shannon's cross-entropy
over the possible information content (Hartley information)
[14, pg. 169],[26, pp. 228-229]:
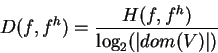 |
(22) |
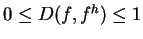 characterizes the percentage of information lost for fh
representing distribution f.
characterizes the percentage of information lost for fh
representing distribution f.



Next: Search through Model-Space:
Up: Reconstructability Analysis (RA)
Previous: Join-procedure:
Thomas Prang
1998-06-07
![]() ,
also known as L-norms:
,
also known as L-norms: