


Next: Model Evaluation:
Up: Reconstructability Analysis (RA)
Previous: Formal Definition:
Let
fjoin(i) be the prior distribution from (i-1) previous
joins,
Vjoin(i) the variables set
fjoin(i) is defined on
(letting
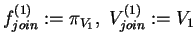 ).
Denote the projection (subrelation, subsystem) whose information is to be added to the join
as
).
Denote the projection (subrelation, subsystem) whose information is to be added to the join
as
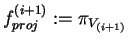 ,
with
Vproj(i):=Vi as its variable set.
The new resulting distribution from this join is
fjoin(i+1) and defined
on the variable set
,
with
Vproj(i):=Vi as its variable set.
The new resulting distribution from this join is
fjoin(i+1) and defined
on the variable set
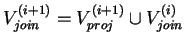 .
We define three sets of variables:
.
We define three sets of variables:
For the join we need to combine the two distributions
fproj(i+1) and
fjoin(i)over their common variable-set B(i). If
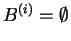 ,
then the distributions
are assumed to be independent (by the model) and we
obtain
fjoin(i+1) by multiplying
,
then the distributions
are assumed to be independent (by the model) and we
obtain
fjoin(i+1) by multiplying
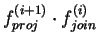 .
Let
.
Let
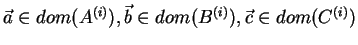 :
:
Otherwise we transform
fjoin(i) into a conditional distribution
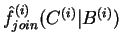 .
For each value
.
For each value
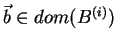 we obtain a conditional distribution on
dom(C(i)) (as described in section 2.3.2) by dividing:
we obtain a conditional distribution on
dom(C(i)) (as described in section 2.3.2) by dividing:
Then we obtain
fjoin(i+1) by:
By the way,
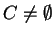 because of the irredundancy condition,
because of the irredundancy condition,
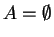 can
be the case in some joins but this does not influence the described procedure.
can
be the case in some joins but this does not influence the described procedure.
Performing relational joins for
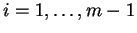 we combine the information of all
projections together and in most cases end
up with the maximum entropy restruction
we combine the information of all
projections together and in most cases end
up with the maximum entropy restruction
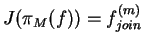 of our simplified structure-system
of our simplified structure-system 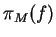 .
.
In some cases, when we have a so called ``loop-structure'' which means loop-dependencies
in our model-structure, then
fjoin(m) is only an approximation of
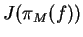 .
As
.
As
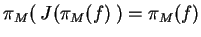 ,
we can recognize such a situation by simply
projecting
fjoin(m) into our model.
If there are loop-dependencies we need to continue joining the projections
,
we can recognize such a situation by simply
projecting
fjoin(m) into our model.
If there are loop-dependencies we need to continue joining the projections
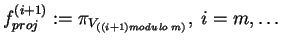 to our already obtained join-distribution
fjoin(m) until we reach a close
enough approximation of
to our already obtained join-distribution
fjoin(m) until we reach a close
enough approximation of
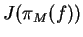 .
This can be done following the above discussed
procedures. Note that
.
This can be done following the above discussed
procedures. Note that
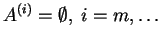 .
.
is a measure for the closeness of the approximation [26, pp. 225-227]:
For examples on the described join procedures see also [26, pp. 223-227].



Next: Model Evaluation:
Up: Reconstructability Analysis (RA)
Previous: Formal Definition:
Thomas Prang
1998-06-07
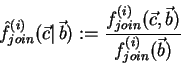
![]() we combine the information of all
projections together and in most cases end
up with the maximum entropy restruction
we combine the information of all
projections together and in most cases end
up with the maximum entropy restruction
![]() of our simplified structure-system
of our simplified structure-system ![]() .
.
![]() .
As
.
As
![]() ,
we can recognize such a situation by simply
projecting
fjoin(m) into our model.
If there are loop-dependencies we need to continue joining the projections
,
we can recognize such a situation by simply
projecting
fjoin(m) into our model.
If there are loop-dependencies we need to continue joining the projections
![]() to our already obtained join-distribution
fjoin(m) until we reach a close
enough approximation of
to our already obtained join-distribution
fjoin(m) until we reach a close
enough approximation of
![]() .
This can be done following the above discussed
procedures. Note that
.
This can be done following the above discussed
procedures. Note that
![]() .
.