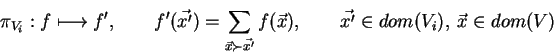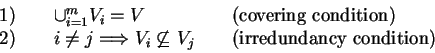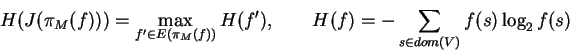


Next: Join-procedure:
Up: Reconstructability Analysis (RA)
Previous: Informal Introduction:
Let me now formally define Reconstructability Analysis formally.
Define
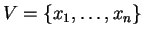 to be the set of all dimensions.
The domain of V is the cartesian product of the domains of its dimensions:
to be the set of all dimensions.
The domain of V is the cartesian product of the domains of its dimensions:
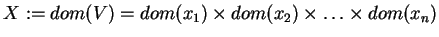 .
On this domain the
database induces a count-table and a probability-distribution
.
On this domain the
database induces a count-table and a probability-distribution
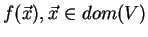 (Section 2.1) which represents the information and relationship
among the variables, P denotes the set of all probability distributions
defined on dom(V):
(Section 2.1) which represents the information and relationship
among the variables, P denotes the set of all probability distributions
defined on dom(V):
A projection as described in Section 2.3.1
of f onto
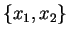 is denoted
is denoted
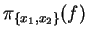 ,
,
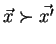 means vector-inclusion:
means vector-inclusion:
A model of V, the overall variable-set, is defined as a set of subsets of V
such that:
The projection of f onto a model M is called a ``structure system''
and consist of the set of distributions:
As a structure system, 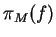 is a simplified representation of the overall system f,
it corresponds to and could be projected from a set of possible overall systems.
The set of overall probability distributions which are compatible with a given
structure-system
is a simplified representation of the overall system f,
it corresponds to and could be projected from a set of possible overall systems.
The set of overall probability distributions which are compatible with a given
structure-system 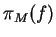 is called its ``reconstruction family'':
is called its ``reconstruction family'':
The maximum entropy reconstruction of a structure-system 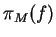 is the
unique overall distribution which can be rebuilt without adding any
extra knowledge (unbiased) and is defined as
is the
unique overall distribution which can be rebuilt without adding any
extra knowledge (unbiased) and is defined as
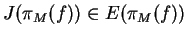 such that
such that
This maximum entropy reconstruction can be obtained by a series
of relational join operations (
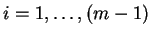 )
in which we sequentially add
the knowledge of the subrelations to form the overall system.
)
in which we sequentially add
the knowledge of the subrelations to form the overall system.



Next: Join-procedure:
Up: Reconstructability Analysis (RA)
Previous: Informal Introduction:
Thomas Prang
1998-06-07