Analysis of Variance (ANOVA)

Analysis of Variance is a statistical method for modeling the effect of several nominal input variables and their interactions on an continuous, ordered output variable. The F-test is used for controlling if the influence of some input variables, alone or interacting, is significant on the output variable. Least Squares estimates are used to estimate the strength of the effect. [8, pp. 108-145], [19,34,21,22]

A good example is the growth of plants. We want to investigate if there is an influence on the growth of plants by growing them on different types of soil, using different fertilizer, etc. and if there are interacting influences among these variables. Here the kind of soil, fertilizer, etc. are the nominal input variables, and the height of the growing plants might be the output variable.

We can also use Analysis of Variance for our purely nominal domain. In this case the modeled continuous output variable corresponds to a probability distribution over the nominal relation. We model the likelihood that specific value combinations appear together.

Analysis of Variance is used to investigate the probability distribution by searching for patterns of values that occur together. The focus is on finding out which values and variables appear together in a random manner (no structure) and what specific values have a strong influence either in combination or on its own on the likelihood to appear. In other words are some dimensions independent from each other or is there a ``correlation'' effect between the variables. In an example we might want to investigate the influences of a patient's blood type, of a new medication versus its placebo, of the occurrence or non-occurrence of some Genes in his DNA, of the climate he lives in, etc., on the patient's probability of healing or not healing.

Let me formally introduce the model for three variables x₁,x₂,x₃:

$$f_{ijk} = \mu + A_i + B_j + C_k + AB_{ij} + AC_{ik} + BC_{jk} + ABC_{ijk} + \epsilon_{ijk}$$

where f_ijk denotes the output-variable (probability) for the i-th value of variable x₁, the j-th value of the second variable x₂ and the k-th value of x₃. Let $\mu$ be the overall mean of the output-variable, which would be the random-probability $(1/ \vert dom(x_1 \times x_2 \times x_3) \vert )$ in our case. A_i is defined as the influence of the i-th value of the first variable, B_j as the influence of the j-th value of the second variable, and C_k as the influence of the k-th value of the third variable. AB_ij, AC_ik, BC_jk and ABC_ijkare the combined effects due to some of the values occurring together. For example, a specific soil-type (x₁=1) and a specific fertilizer (x₂=1) may have only a very small or even negative influence on the plant-growth compared to the average growth ( A₁ < 0, B₁< 0), but in combination they have a big positive effect ( $AB_{11}\gg 0$).

$\epsilon_{ijk}$ consists of all the effects of other variables which we ignored in our model. It is referred to as a ``residual'' and it can be interpreted as the random error of the model. In the Analysis of Variance the random errors $\epsilon_{ijk}$ are assumed to be independent, normally distributed random variables with mean 0 and the same variance ( $\epsilon_{ijk} \sim N(0,\sigma^2)),\;$ for all i,j,k. That means we assume only a linear influence ( A_i,B_j,C_k,AB_ij, etc.) on the system-function f_ijk and no change in variation. For example, a specific medication might have a positive effect on the health of patients, while placebos might have a smaller effect. Nevertheless, the variability of health over patients taking medication or placebos is assumed to be the same. If this is not the case then we are perhaps missing another variable (belief in placebo?) which explains and separates an increased variation.

Because of the definition of $\mu$ as the mean-value and $\epsilon_{ijk}$ as random variations with mean 0, the following constraints also hold for our model:

$$\sum_i A_i = \sum_j B_j = \sum_k C_k = 0$$

$$\sum_{ij} AB_{ij} = \sum_{ik} AC_{ik} = \sum_{jk} BC_{jk} = 0$$

$$\sum_{ijk} ABC_{ijk} = 0$$

With these assumptions we can compute the following least-square estimates of the variable effects. Let f_ijk be the actual output values (probabilities) for the i-th, j-th, and k-th value of the respective input-variables, a ``<sub>.</sub>'' denotes a subscript over which the average is taken, `` $\,\hat{\ }\,$'' denotes an estimate:

$$\hat{\mu} = f_{...}$$

$$\hat{A_i} = f_{i..} - f_{...}$$

$$\hat{B_j} = f_{.j.} - f_{...}$$

$$\hat{C_k} = f_{..k} - f_{...}$$

$$\widehat{AB_{ij}} = f_{ij.} - f_{i..} - f_{.j.} + f_{...}$$

$$\widehat{AC_{ik}} = f_{i.k} - f_{i..} - f_{..k} + f_{...}$$

$$\widehat{AB_{jk}} = f_{.jk} - f_{.j.} - f_{..k} + f_{...}$$

$$\widehat{ABC_{ijk}} = f_{ijk} - f_{ij.} - f_{i.k} - f_{.jk} + f_{i..} + f_{.j.} + f_{..k} - f_{...}$$

These estimates can be generalized for more variables.

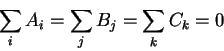
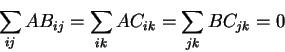
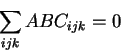
The F-ratio test is used to test if interactions between variables like (AB_ij, for all i,j) are significant and if we need to include them in our model. Above I presented a complete model with all possible interactions of three variables, but in reality we often want to represent only the significant aspects. For more details on the F-ratio test see [19,34,8].

A random distribution with no structure is equivalent to all variables not having any direct influence on the distribution and only the global mean of the model being needed to ``explain'' everything. If the distribution is not random then the structure can be due to the influence of some single variables and/or to some more complex interactions. These kinds of interactions are the structures we are especially interested in and which we try to capture by doing analysis of variance.

Comparing Analysis of Variance to the basic techniques, we recognize that marginal distributions of variables (for example f_..k) are used to estimate their influence on the overall probability-distribution. First we project on the variables of interest then we take the averaged probability of the values of interest. For example to get the influence of the i-th value of variable x₁ we project on variable x₁, take the probability for the i-th value, which is the sum of all probabilities where the i-th value of x₁ occurs, and divide it by $\vert dom(x_2 \times x_3) \vert$ to obtain the average probability. Then we subtract the global mean $\mu$ and end up with the influence A_i.

Some of these issues will be discussed in more detail in the following section. Reconstructability Analysis is basically used for the same purpose but is more precise than ANOVA, as no model assumptions are made about how the data influences the output variable [21,22]. This is also the reason for this rather short introduction into ANOVA while the discussion of Reconstructability Analysis will be much more detailed.