


Next: Transmission
Up: Information and Uncertainty Measures
Previous: Probabilistic Interpretation of the
Shannon's Entropy
In 1948 Shannon introduced a general uncertainty-measure on random variables
which takes different probabilities among states into account [40, pp. 392-396].
Today this measure is well known as ``Shannon's Entropy'' [26, pp. 112-116],
[28, pp. 153-167], etc.
Let X be a random-variable and P the space of all finite probability-distributions:
 |
(8) |
where dom(X) is the value-set of variable X, 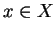 a specific value and f the
probability-distribution of X.
a specific value and f the
probability-distribution of X.
The conditional entropy of a variable Y knowing variable X is
defined as the average of the entropies of Y for each value 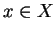 ,
weighted according to the probability that x occurs:
,
weighted according to the probability that x occurs:
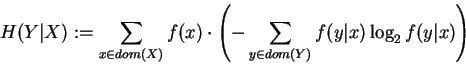 |
(9) |
where f(y|x) denotes the conditional probability of 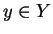 when variable
X is in state x.
The conditional entropy expresses how uncertain we are of Y the average when
we know X (which could be any of the values
when variable
X is in state x.
The conditional entropy expresses how uncertain we are of Y the average when
we know X (which could be any of the values 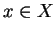 ).
).
Shannon's entropy is an important measure for evaluating structures and patterns in our
data. The lower the entropy (uncertainty) the more structure is
already given in the relation.
The usability becomes more obvious by looking at some properties of Shannon's Entropy:
- 1.
- H=0 if and only if f(s)=1 for one
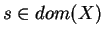 and f(x)=0 for
all other
and f(x)=0 for
all other
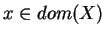 .
This means the entropy H is only 0 if we are certain about the outcome.
.
This means the entropy H is only 0 if we are certain about the outcome.
- 2.
- For any number of states
N=|dom(X)| the entropy H is maximal and equal to
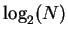 if all states
if all states
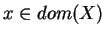 have equal probability (Hartley-information).
This is the situation where we have no structure in our distribution and are
most uncertain.
have equal probability (Hartley-information).
This is the situation where we have no structure in our distribution and are
most uncertain.
- 3.
- Any change toward equalization of the probabilities increases H. The more
the states are equally likely to occur the less structure we have and the
higher the uncertainty.
- 4.
- The uncertainty of two independent variables (X,Y) is the sum of their respective
uncertainties. This conforms with the initial comments we gave about
the Hartley information-measure.
Knowing X gives us no information about Y; therefore the
conditional entropy Y knowing X equals the entropy of Y:
HX(Y) = H(Y)
- 5.
- The uncertainty of two dependent variables (X,Y) is less than the sum of the
individual uncertainties. This is caused by the information (structure)
which is given in the correlation of the two variables.
Because of the structure relating Y and X, the conditional entropy
Y knowing X is smaller than the `a priori' entropy of Y:
HX(Y) < H(Y)
- 6.
- The uncertainties of two variables (X,Y) is the sum of the uncertainty of one
variable X added to the conditional uncertainty of the other variable Y knowing X.
This also shows that the uncertainty of a variable Y is never increased by
knowledge of X:
H(X, Y) = H(X) + HX(Y)
In connection with Shannon's entropy there are several similar measures defined.
A relative uncertainty of a variable, also called normalized uncertainty, is obtained by
dividing by the maximum uncertainty
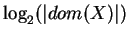 :
:
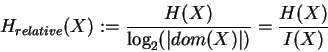 |
(10) |



Next: Transmission
Up: Information and Uncertainty Measures
Previous: Probabilistic Interpretation of the
Thomas Prang
1998-06-07
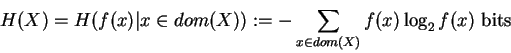
![]() ,
weighted according to the probability that x occurs:
,
weighted according to the probability that x occurs:
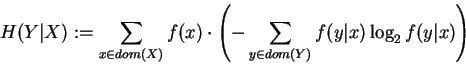
![]() :
: