


Seien R und S zwei Relationen mit den Schemata
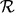 und
und
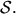
Sei 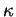 Primärschlüssel von
Primärschlüssel von
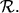
Dann ist
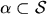 ein Fremdschlüssel,
wenn für alle
Tupel s
ein Fremdschlüssel,
wenn für alle
Tupel s 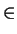 S gilt:
S gilt:
- s.
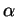 enthält entweder nur Nullwerte oder nur Werte ungleich Null
enthält entweder nur Nullwerte oder nur Werte ungleich Null
- Enthält s.
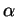 keine Nullwerte, existiert ein Tupel r
keine Nullwerte, existiert ein Tupel r 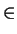 R mit
s.
R mit
s.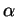 = r.
= r.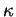
Die Erfüllung dieser Eigenschaft heißt referentielle Integrität. Die
Attribute von Primär- und Fremdschlüssel haben jeweils dieselbe Bedeutung und
oft auch dieselbe Bezeichnung (falls möglich).
Ohne Überprüfung der referentiellen Integrität
kann man leicht einen inkonsistenten Zustand der Datenbasis erzeugen,
indem z. B. eine Vorlesung mit nichtexistentem Dozenten eingefügt wird.
Zur Gewährleistung der
referentiellen Integrität muß also beim Einfügen, Löschen und Ändern immer
sichergestellt sein, daß gilt
Erlaubte Änderungen sind daher:
- Einfügen eines Tupels in S verlangt, daß der Fremdschlüssel auf
ein existierendes Tupel in R verweist.
- Ändern eines Tupels in S verlangt, daß der neue Fremdschlüssel
auf ein existierendes Tupel in R verweist.
- Ändern eines Primärschlüssels in R verlangt, daß kein Tupel
aus S auf ihn verwiesen hat.
- Löschen eines Tupels in R verlangt, daß kein Tupel aus S auf ihn
verwiesen hat.



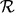 und
und
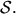
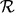 und
und
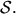
![]() Primärschlüssel von
Primärschlüssel von
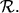
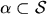 ein Fremdschlüssel,
wenn für alle
Tupel s
ein Fremdschlüssel,
wenn für alle
Tupel s ![]() S gilt:
S gilt: