Das im Initialentwurf erzeugte relationale Schema läßt sich verfeinern, indem einige der 1 : 1-, 1 : N- oder N : 1-Beziehungen eliminiert werden. Dabei dürfen nur Relationen mit gleichem Schlüssel zusammengefaßt werden.
Nach dieser Regel können von den drei Relationen
| Vorlesungen | : | {[ VorlNr : integer, Titel : string, SWS : integer] } |
| Professoren | : | {[ PersNr : integer, Name : string, Rang : string, Raum : integer] } |
| lesen | : | {[ PersNr : integer, VorlNr : integer] } |
die Relationen Vorlesungen und lesen zusammengefaßt werden. Somit verbleiben im Schema
| Vorlesungen | : | {[ VorlNr : integer, Titel : string, SWS : integer, gelesenVon : integer] } |
| Professoren | : | {[ PersNr : integer, Name : string, Rang : string, Raum : integer] } |
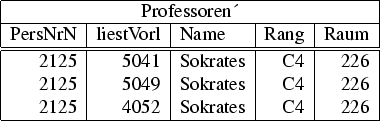
Das Zusammenlegen von Relationen mit unterschiedlichen Schlüsseln erzeugt eine Redundanz von Teilen der gespeicherten Information. Beispielsweise speichert die (unsinnige) Relation
| Professoren' | : | {[ PersNr, liestVorl, Name, Rang, Raum ] } |
zu jeder von einem Professor gehaltenen Vorlesung seinen Namen, seinen Rang und sein Dienstzimmer:

Bei 1 : 1-Beziehungen gibt es zwei Möglichkeiten, die ursprünglich entworfene Relation mit den beteiligten Entity-Typen zusammenzufassen.
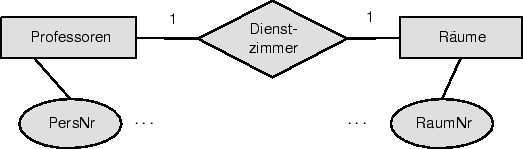
Abbildung 6.2 zeigt eine mögliche Modellierung für die Unterbringung von Professoren in Räumen als 1 : 1-Beziehung. Die hierzu gehörenden Relationen heißen
| Professoren | : | {[ PersNr, Name, Rang ] } |
| Räume | : | {[ RaumNr, Größe, Lage ] } |
| Dienstzimmer | : | {[ PersNr, RaumNr ] } |
Da Professoren und Dienstzimmer denselben Schlüssel haben, kann zusammengefaßt werden zu
| Professoren | : | {[ PersNr, Name, Rang, Raum] } |
| Räume | : | {[ RaumNr, Größe, Lage ] } |
Da das Attribut RaumNr innerhalb der Relation Dienstzimmer ebenfalls einen Schlüssel bildet, könnten als Alternative auch die Relationen Dienstzimmer und Räume zusammengefaßt werden:
| Professoren | : | {[ PersNr, Name, Rang] } |
| Räume | : | {[ RaumNr, Größe, Lage, ProfPersNr ] } |
Diese Modellierung hat allerdings den Nachteil, daß viele Tupel einen sogenannten Nullwert für das Attribut ProfPersNr haben, da nur wenige Räume als Dienstzimmer von Professoren genutzt werden.
Die in Abbildung 6.1 gezeigte Generalisierung von Assistenten und Professoren zu Angestellte könnte wie folgt durch drei Relationen dargestellt werden:
| Angestellte | : | {[ PersNr, Name] } |
| Professoren | : | {[ PersNr, Rang, Raum] } |
| Assistenten | : | {[ PersNr, Fachgebiet] } |
Hierdurch wird allerdings die Information zu einem Professor, wie z.B.
auf zwei Tupel aufgeteilt:
Um die vollständige Information zu erhalten, müssen diese beiden Relationen verbunden werden (Join).
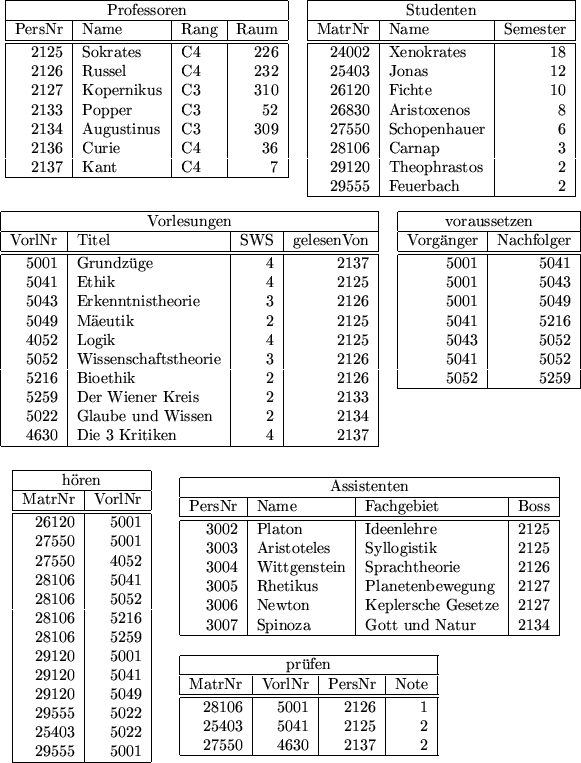
Abbildung 6.3 zeigt eine Beispiel-Ausprägung der Universitäts-Datenbasis. Das zugrundeliegende Schema enthält folgende Relationen:
| Studenten | : | {[ MatrNr : integer, Name : string, Semester : integer] } |
| Vorlesungen | : | {[ VorlNr : integer, Titel : string, SWS : integer, gelesenVon : integer] } |
| Professoren | : | {[ PersNr : integer, Name : string, Rang : string, Raum : integer] } |
| Assistenten | : | {[ PersNr : integer, Name : string, Fachgebiet : string, Boss : integer] } |
| hören | : | {[ MatNr : integer, VorlNr : integer] } |
| voraussetzen | : | {[ Vorgänger : integer, Nachfolger : integer] } |
| prüfen | : | {[ MatrNr : integer, VorlNr : integer, PersNr : integer, Note :decimal] } |
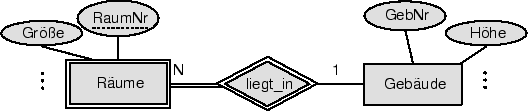
Zur Modellierung von schwachen Entity-Typen betrachten wir Abbildung 6.4, in der mittels der Relation liegt_in der schwache Entitity-Typ Räume dem Entity-Typ Gebäude untergeordnet wurde.
Wegen der 1 : N-Beziehung zwischen Gebäude und Räume kann die Beziehung liegt_in verlagert werden in die Relation Räume:
Ein Beziehung bewohnt zwischen Professoren und Räume benötigt als Fremdschlüssel zum einen die Personalnummer des Professors und zum anderen die Kombination von Gebäude-Nummer und Raum-Nummer:
Da bewohnt eine 1 : 1-Beziehung darstellt, kann sie durch einen Fremdschlüssel beim Professor realisiert werden. Ist die beim Gebäude hinterlegte Information eher gering, käme auch, wie im Universitätsschema in Abbildung 6.1 gezeigt, ein Attribut Raum bei den Professoren infrage.