Definition

Gegeben sind n nicht notwendigerweise unterschiedliche Wertebereiche (auch Domänen genannt) D₁,..., D_n, welche nur atomare Werte enthalten, die nicht strukturiert sind, z.B. Zahlen oder Strings.

Eine Relation R ist definiert als Teilmenge des kartesischen Produkts der n Domänen:

R $$\subseteq$$ D₁ x D₂ x...x D_n

Es wird unterschieden zwischen dem Schema einer Relation, gegeben durch die n Domänen und der aktuellen Ausprägung (Instanz). Ein Element der Menge R wird als Tupel bezeichnet, dessen Stelligkeit sich aus dem Relationenschema ergibt. Wir bezeichnen mit sch( R) oder mit 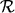= A₁,..., A_n die Menge der Attribute und mit R die aktuelle Ausprägung. Mit dom( A) bezeichnen wird die Domäne eines Attributs A. Also gilt

R $$\subseteq$$ dom(A₁) x dom(A₂) x...x dom(A_n)

Im Datenbankbereich müssen die Domänen außer einem Typ noch einen Namen haben. Wir werden Relationenschemata daher durch eine Folge von Bezeichner/Wertebereich - Tupeln spezifizieren, z.B.

Telefonbuch : { [Name : string, Adresse: string, TelefonNr : integer ] }

Hierbei wird in den eckigen Klammern [ ... ] angegeben, wie die Tupel aufgebaut sind, d.h. welche Attribute vorhanden sind und welchen Wertebereich sie haben. Ein Schlüsselkandidat wird unterstrichen. Die geschweiften Klammern { ... } sollen ausdrücken, daß es sich bei einer Relationenausprägung um eine Menge von Tupeln handelt. Zur Vereinfachung wird der Wertebereich auch manchmal weggelassen:

Telefonbuch : { [Name, Adresse, TelefonNr ] }