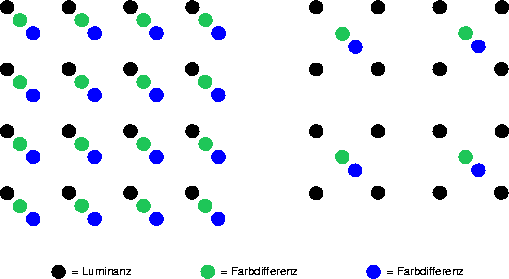
Zunächst wird das RGB-Bild in den YUV-Raum transformiert.
Da das Auge für Helligkeitssprünge sensitiver ist als für
Farbdifferenzen, kann man nun die ![]() -Matrix in der vollen
Auflösung belassen und in den U, V-Matrizen jeweils 4 Pixel mitteln
(4:1:1 Subsampling).
-Matrix in der vollen
Auflösung belassen und in den U, V-Matrizen jeweils 4 Pixel mitteln
(4:1:1 Subsampling).
Für je 4 Originalpixel mit insgesamt 12 Bytes werden nun
![]() Bytes benötigt (pro Bildpunkt also
Bytes benötigt (pro Bildpunkt also
![]() Bit).
Die Reduktion beträgt 50 %.
Bit).
Die Reduktion beträgt 50 %.
Beim JPEG-Verfahren werden nun die drei Matrizen in
Blöcke mit ![]() Abtastwerten aufgeteilt.
Anschließend durchlaufen die Blöcke folgende Schritte:
Abtastwerten aufgeteilt.
Anschließend durchlaufen die Blöcke folgende Schritte:
Durch die Wahl der Rundungstabelle läßt sich der Tradeoff
zwischen Qualität und Kompression beliebig steuern.
Ein typisches Farbbild läßt sich ohne für das Auge
sichtbare Artefakte auf 10 % seiner
Originalgröße reduzieren.
Eine Reduktion auf 5 % verursacht oft nur leichte,
kaum wahrnehmbare Verzerrungen.
DCT (Diskrete Cosinus Transformation)
Die diskrete Cosinus-Transformation ist ein Spezialfall
der Fouriertransformation.
Es wird ausgenutzt, daß für ``gerade'' Funktionen
(d.h. ![]() ) der Sinus-Term mit seinem imaginären
Anteil wegfällt.
Ein zweidimensionaler Bildbereich läßt sich durch Spiegelung an der
) der Sinus-Term mit seinem imaginären
Anteil wegfällt.
Ein zweidimensionaler Bildbereich läßt sich durch Spiegelung an der
![]() -Achse künstlich gerade machen.
-Achse künstlich gerade machen.
Hierdurch wird eine ![]() Ortsmatrix in eine
Ortsmatrix in eine
![]() Frequenzmatrix transformiert.
Frequenzmatrix transformiert.
Mit Hilfe der inversen DCT lassen sich die Originalwerte rekonstruieren.
![\begin{displaymath}
f[x,y] :=
\frac{1}{4} \sum_{u = 0}^{7} \ \
\sum_{v = 0}^{7...
...dot \pi}{16} \cdot \cos
\frac{(2 y + 1) \cdot v \cdot \pi}{16}
\end{displaymath}](img414.gif)
Für die Bildverarbeitung wird der Pixelwertebereich
![]() in das symmetrische Intervall
in das symmetrische Intervall
![]() verschoben.
Der Wertebereich von
verschoben.
Der Wertebereich von ![]() liegt dann im Intervall
liegt dann im Intervall
![]() .
Der errechnete Koeffizient
.
Der errechnete Koeffizient ![]() entspricht
dem Anteil der Frequenz null in beiden Achsen und wird DC-Koeffizient
(Gleichspannungsanteil) bezeichnet.
Die übrigen Koeffizienten werden
entspricht
dem Anteil der Frequenz null in beiden Achsen und wird DC-Koeffizient
(Gleichspannungsanteil) bezeichnet.
Die übrigen Koeffizienten werden ![]() -Koeffizienten
(Wechselspannungsanteil) genannt.
Z.B. bezeichnet
-Koeffizienten
(Wechselspannungsanteil) genannt.
Z.B. bezeichnet ![]() die höchste, in beiden Richtungen
auftretende Frequenz.
die höchste, in beiden Richtungen
auftretende Frequenz.
Die Eingangsmatrix ![]() läßt sich auch durch
läßt sich auch durch
![]() transformieren mit Hilfe der Matrix
transformieren mit Hilfe der Matrix ![]() :
:
0cm
| 0.353553 | 0.353553 | 0.353553 | 0.353553 | 0.353553 | 0.353553 | 0.353553 | 0.353553 | |
| 0.490393 | 0.415735 | 0.277785 | 0.097545 | -0.097545 | -0.277785 | -0.415735 | -0.490393 | |
| 0.461940 | 0.191342 | -0.191342 | -0.461940 | -0.461940 | -0.191342 | 0.191342 | 0.461940 | |
| 0.415735 | -0.097545 | -0.490393 | -0.277785 | 0.277785 | 0.490393 | 0.097545 | -0.415735 | |
| 0.353553 | -0.353553 | -0.353553 | 0.353553 | 0.353553 | -0.353553 | -0.353553 | 0.353553 | |
| 0.277785 | -0.490393 | 0.097545 | 0.415735 | -0.415735 | -0.097545 | 0.490393 | -0.277785 | |
| 0.191342 | -0.461940 | 0.461940 | -0.191342 | -0.191342 | 0.461940 | -0.461940 | 0.191342 | |
| 0.097545 | -0.277785 | 0.415735 | -0.490393 | 0.490393 | -0.415735 | 0.277785 | -0.097545 |
Quantisierung
Die errechnete Matrix hat von links oben nach rechts unten Werte
abnehmender Größe.
Da die Werte rechts unten den hohen, eher unwichtigen Frequenzen
entsprechen, werden alle Einträge mit Faktoren zunehmender Größe
dividiert.
0cm to 17cm
|
|
to 17cm
|
|
| 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | |
| 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | |
| 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | |
| 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
| 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | |
| 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 | |
| 15 | 17 | 19 | 21 | 23 | 25 | 27 | 29 | |
| 17 | 19 | 21 | 23 | 25 | 27 | 29 | 31 |
Die AC-Koeffizienten werden zunächst in eine Zick-Zack-Sequenz umgeordnet:
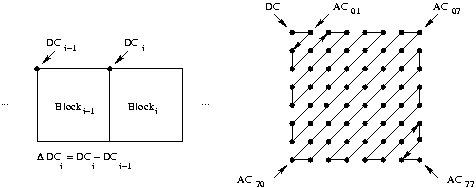
Die AC-Koeffizienten längs dieses Weges bis zum letzten Eintrag ungleich Null werden als Folge von Paaren beschrieben:
| Symbol 1: | Länge der ununterbrochenen Folge von Nullen vor diesem Wert (Runlength) | |
| Anzahl der Bits, die zur Darstellung des Wertes erforderlich sind. | ||
| Symbol 2: | der Wert selbst | |
Der quantisierte DCT-Koeffizient ![]() aus vorigem
Beispiel wird beschrieben als Tupel
aus vorigem
Beispiel wird beschrieben als Tupel ![]() ,
denn vor ihm in der Zickzacksequenz stehen 11 Nullen,
sein Wert kann mit 2 Bit codiert werden,
und sein Wert beträgt
,
denn vor ihm in der Zickzacksequenz stehen 11 Nullen,
sein Wert kann mit 2 Bit codiert werden,
und sein Wert beträgt ![]() .
.
Für das Symbol 1 gibt es Häufigkeitsverteilungen,
aus denen sich ein Huffman-Code konstruieren läßt.
Für das Symbol 2 wählt man ein 2-er Komplement,
welches berücksichtigt, daß bei angekündigten
![]() Bits nur solche Zahlen kodiert werden müssen, für
die
Bits nur solche Zahlen kodiert werden müssen, für
die ![]() Bits nicht ausreichen.
Bits nicht ausreichen.
für Symbol 1
|
für Symbol 2
|
| Huffman | 2-er Komplement | |||
| Symbol 1 | Symbol 2 | für Symbol 1 | für Symbol 2 | |
| (1, 3) | -7 | 1111001 | 000 | |
| (0, 4) | -12 | 1011 | 0011 | |
| (0, 4) | -8 | 1011 | 0111 | |
| (0, 1) | -1 | 00 | 0 | |
| (1, 1) | 1 | 1100 | 1 | |
| (0, 3) | 7 | 100 | 111 | |
| (0, 3) | -5 | 100 | 010 | |
| (0, 3) | -7 | 100 | 000 | |
| (0, 2) | -3 | 01 | 00 | |
| (1, 1) | 1 | 1100 | 1 | |
| (3, 1) | -1 | 111010 | 0 | |
| (1, 2) | -3 | 11011 | 00 | |
| (0, 3) | -4 | 100 | 011 | |
| (0, 1) | -1 | 00 | 0 | |
| (0, 3) | 4 | 100 | 100 | |
| (0, 2) | 3 | 01 | 11 | |
| (11, 2) | -3 | 1111111111010000 | 00 | |
| (0, 1) | 1 | 00 | 1 | |
| (0, 1) | -1 | 00 | 0 | |
| EOB | 1010 |
|
|
| 95 | 88 | 87 | 95 | 88 | 95 | 95 | 95 |
| 143 | 144 | 151 | 151 | 153 | 170 | 183 | 181 |
| 153 | 151 | 162 | 166 | 162 | 151 | 126 | 117 |
| 143 | 144 | 133 | 130 | 143 | 153 | 159 | 175 |
| 123 | 112 | 116 | 130 | 143 | 147 | 162 | 189 |
| 133 | 151 | 162 | 166 | 170 | 188 | 166 | 128 |
| 160 | 168 | 166 | 159 | 135 | 101 | 93 | 98 |
| 154 | 155 | 153 | 144 | 126 | 106 | 118 | 133 |
| 01011111 | 01011000 | 01010111 | 01011111 | 01011000 | 01011111 | 01011111 | 01011111 |
| 10001111 | 10010000 | 10010111 | 10010111 | 10011001 | 10101010 | 10110111 | 10110101 |
| 10011001 | 10010111 | 10100010 | 10100110 | 10100010 | 10010111 | 01111110 | 01110101 |
| 10001111 | 10010000 | 10000101 | 10000010 | 10001111 | 10011001 | 10011111 | 10101111 |
| 01111011 | 01110000 | 01110100 | 10000010 | 10001111 | 10010011 | 10100010 | 10111101 |
| 10000101 | 10010111 | 10100010 | 10100110 | 10101010 | 10111100 | 10100110 | 10000000 |
| 10100000 | 10101000 | 10100110 | 10011111 | 10000111 | 01100101 | 01011101 | 01100010 |
| 10011010 | 10011011 | 10011001 | 10010000 | 01111110 | 01101010 | 01110110 | 10000101 |
1111001000101100111011011100011001100111100010100000010011001
1110100110110010001100010010001111111111111010000000010001010

100% |

9% |

5% |

4% |

3%

2%

1.5%

1%
![]()
![]()
![]()
![]()