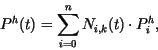
Über die Eigenschaften der B-Splines hinaus, wäre für den 3D-Fall auch eine Invarianz unter projektiven Abbildungen wünschenswert, da dort die 3D-Kurven auf den 2D-Bildschirm projeziert werden müssen.
Um möglichst große Freiheit bei den zu appxroximierenden Formen zu haben, sollten die Kurven beliebige Kegelschnitte (insbesondere Kreise) annähern können.
Beide Wünsche werden von der allgemeinsten Form zum Zeichnen von Kurven erfüllt. Es handelt sich dabei um NURBS (nonuniform rational basis splines).
Es handelt sich wieder um eine baryzentrische Kombination:
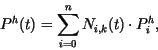
wobei hier die ![]() mit homogener Koordinate eingehen (
mit homogener Koordinate eingehen (
![]() ) und die Punkte der Kurve
) und die Punkte der Kurve ![]() ggf. eine von
ggf. eine von ![]() verschiedene
homogene Koordinate erhalten.
Um die Kurve zeichnen zu können, müssen wir sie in die euklidische Ebene
projizieren.
Dies geschieht durch die Abbildung vom dreidimensionalen Raum der homogenen
Koordinaten in die zweidimensionale euklidische Ebene.
Da sich für einen Punkt in homogenen Koordinaten seine Position in der
euklidischen Ebene ergibt, wenn man mit der homogenen Koordinate
verschiedene
homogene Koordinate erhalten.
Um die Kurve zeichnen zu können, müssen wir sie in die euklidische Ebene
projizieren.
Dies geschieht durch die Abbildung vom dreidimensionalen Raum der homogenen
Koordinaten in die zweidimensionale euklidische Ebene.
Da sich für einen Punkt in homogenen Koordinaten seine Position in der
euklidischen Ebene ergibt, wenn man mit der homogenen Koordinate ![]() normiert, ergeben sich die Gewichtungsfunktionen als Quotient zweier Polynome.
Deswegen heißen diese Kurven rational:
normiert, ergeben sich die Gewichtungsfunktionen als Quotient zweier Polynome.
Deswegen heißen diese Kurven rational:
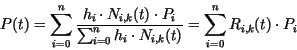
mit
![]() und P(t) zweidimensional und
und P(t) zweidimensional und
Die ![]() werden auch homogene Gewichte oder nur Gewichte
genannt, weil sie zusätzlichen Einfluß auf den Verlauf der Kurve
ausüben. Für einen offenen uniformen Knotenvektor
werden auch homogene Gewichte oder nur Gewichte
genannt, weil sie zusätzlichen Einfluß auf den Verlauf der Kurve
ausüben. Für einen offenen uniformen Knotenvektor
![]() mit
mit ![]() und
und ![]() und Gewichten
und Gewichten
![]() ergeben sich die folgenden Kurven, wenn
ergeben sich die folgenden Kurven, wenn ![]() die Werte
die Werte ![]() ,
,
![]() ,
, ![]() und
und ![]() annimmt:
annimmt:
Je größer ![]() wird, umso stärker zihet der Punkt
wird, umso stärker zihet der Punkt ![]() die Kurve an.
Wenn
die Kurve an.
Wenn ![]() sich Null nähert, wird der Einfluß von
sich Null nähert, wird der Einfluß von ![]() immer schwächer.
Für
immer schwächer.
Für ![]() hat
hat ![]() gar keinen Einfluß mehr. Das bedeutet, daß
gar keinen Einfluß mehr. Das bedeutet, daß ![]() mit Berücksichtigung der homogenen Koordinate im Unendlichen liegt.
mit Berücksichtigung der homogenen Koordinate im Unendlichen liegt.