Das Auge kann bei normalen Lichtverhältnissen Details unterscheiden, die mindestens eine Bogenminute (
Wenn einerseits die beiden ''Farben'' Schwarz und Weiß zur Färbung der
Objekte nicht ausreichen, andererseits der Bildschirm aber nur
schwarze Pixel darstellen kann, wird wieder zu einem Trick gegriffen, bei dem
das menschliche Auge betrogen wird.
Das Auge kann bei normalen Lichtverhältnissen Details unterscheiden, die
mindestens eine Bogenminute (![]() Grad) auseinander liegen.
Wenn man in eine weiße Fläche eine
Anzahl
Grad) auseinander liegen.
Wenn man in eine weiße Fläche eine
Anzahl ![]() von nicht benachbarten schwarzen Punkten hineinzeichnet und
diese Fläche dann aus
grösserer Entfernung betrachtet, dann ist das Auge nicht mehr in der Lage,
die einzelnen Punkte voneinander zu unterscheiden.
Die schwarzen und weißen Bereiche werden vom Auge integriert und dadurch
entsteht der Eindruck einer grauen Fläche. Je größer
von nicht benachbarten schwarzen Punkten hineinzeichnet und
diese Fläche dann aus
grösserer Entfernung betrachtet, dann ist das Auge nicht mehr in der Lage,
die einzelnen Punkte voneinander zu unterscheiden.
Die schwarzen und weißen Bereiche werden vom Auge integriert und dadurch
entsteht der Eindruck einer grauen Fläche. Je größer ![]() ist, desto
dunkler wirkt die Fläche. Damit die Fläche gleichmäßig gefärbt
erscheint, wird versucht die Punkte möglichst gleichmäßig zu verteilen.
Eine Möglichkeit dies zu tun, ist das Dithering.
ist, desto
dunkler wirkt die Fläche. Damit die Fläche gleichmäßig gefärbt
erscheint, wird versucht die Punkte möglichst gleichmäßig zu verteilen.
Eine Möglichkeit dies zu tun, ist das Dithering.
Eine ![]() -Dithermatrix
-Dithermatrix ![]() ist mit den
ist mit den ![]() Zahlen
zwischen
Zahlen
zwischen ![]() und
und ![]() besetzt.
Zum Färben einer Fläche mit Grauwert
besetzt.
Zum Färben einer Fläche mit Grauwert
![]() werden
alle Pixel
werden
alle Pixel ![]() gesetzt mit
gesetzt mit
![]() .
Abbildung
4.8
zeigt das Füllmuster zum Schwellwert 7.
.
Abbildung
4.8
zeigt das Füllmuster zum Schwellwert 7.
Die ![]() Zahlen können auf verschiedene Weisen auf die Matrix verteilt
werden. Wir werden die Matrix nach dem Schema des ordered dithering
füllen. Dabei wird die Matrix
Zahlen können auf verschiedene Weisen auf die Matrix verteilt
werden. Wir werden die Matrix nach dem Schema des ordered dithering
füllen. Dabei wird die Matrix ![]() rekursiv aus der Matrix
rekursiv aus der Matrix ![]() gebildet:
gebildet:
Dabei bezeichnet ![]() eine
eine ![]() -Einheitsmatrix; d.h. alle Elemente
der Hauptdiagonalen enthalten eine 1 und die restlichen Elemente sind 0.
-Einheitsmatrix; d.h. alle Elemente
der Hauptdiagonalen enthalten eine 1 und die restlichen Elemente sind 0.
Es ergeben sich:
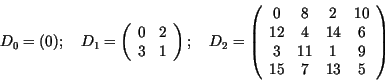

public class DitherMatrix extends NxNMatrix{
/**
* Gibt eine DitherMatrix zurueck, die mit Ditherwerten gefuellt ist.
* @param n die Matrix ist (2 hoch n)x(2 hoch n) Elemente gross und
* enthaelt die (2 hoch 2n) Ditherwerte von 0 bis (2 hoch 2n) - 1.
*/
public DitherMatrix(int n) {
super((int)Math.pow(2,n), 0.0); // mit Nullen fuellen
if(n != 0) { // bei n==0 ist man fertig
DitherMatrix dd = new DitherMatrix(n-1); // 1/4 grosse DitherMatrix
// besorgen und die
fill(0, 0, 0, dd); // Quadranten fuellen: ul
fill(1, 1, 1, dd); // lr
fill(1, 0, 2, dd); // ur
fill(0, 1, 3, dd); // ll
}
}
private void fill(int s, int z, int add, DitherMatrix dd) {
int size = dd.size(); // Ausmasse besorgen
for(int i=0; i < size; i++) { // passenden Quadranten
for(int j=0; j < size; j++) { // fuellen
val[size*z+i][size*s+j]=4*dd.val[i][j] + add;
}
}
}
/**
* Liefert zurueck, ob die Abbildung des uebergebenen Punktes in die
* Matrix auf ein Matrixelement trifft, das kleiner als die uebergebene
* Schwelle ist.
* @param x, y der zu testende Punkt
* @param schwelle der Schwellwert
*/
public boolean kleinerSchwelle(int x, int y, int schwelle) {
if((x < 0) || (y < 0)) { // Wert(e) sinnvoll?
return false; // Falls nicht: Abbruch
}
else { // Sonst: Werte mit Modulo
return (val[x%n][y%n] < schwelle); // in Matrix abbilden und
} // Ergebnis zurueck
}
}
|