Berechnung von Schnittpunkten

Hauptaufgabe eines jeden Ray Tracers ist es, den Schnittpunkt eines Strahls mit einem Objekt zu bestimmen. Man benutzt dazu die parametrisierte Darstellung eines Vektors. Jeder Punkt $(x,y,z)$ auf dem Strahl von $(x_{0}, y_{0}, z_{0})$ nach $(x_{1}, y_{1}, z_{1})$ wird durch einen bestimmten Wert definiert mit

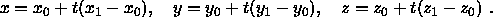
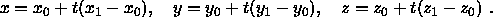
Zur Abkürzung definiert man $\Delta x, \Delta y$ und $\Delta z$ als

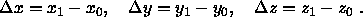
Damit kann man schreiben

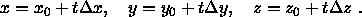
Ist $(x_{0}, y_{0}, z_{0})$ das Projektionszentrum und $(x_{1}, y_{1}, z_{1})$ der Mittelpunkt eines Pixels im Window, so durchläuft $t$ zwischen diesen Punkten die Werte von Null bis Eins. Negative Werte für $t$ liefern Punkte hinter dem Projektionszentrum, Werte größer als Eins stellen Punkte auf der Seite des Windows dar, die vom Projektionszentrum abgewandt ist. Man braucht für jeden Objekttyp eine Darstellung, mit der man den Wert von $t$ am Schnittpunkt des Strahls mit dem Objekt bestimmen kann. Die Kugel bietet sich dafür als eines der einfachsten Objekte an. Aus diesem Grund tauchen Kugeln auch so oft in Ray-Tracing-Bildern auf. Eine Kugel um den Mittelpunkt $(a, b, c)$ und Radius $r$ kann durch die Gleichung

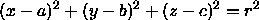
dargestellt werden. Zur Berechnung des Schnittpunkts multipliziert man die Gleichung aus und setzt $x, y$ und $z$ aus der Gleichung von oben ein.

Man erhält eine quadratische Gleichung in $t$, deren Koeffizienten nur die Konstanten aus den Gleichungen der Kugel und des Strahls enthalten. Man kann sie also mit der Lösungsformel für quadratische Gleichungen lösen. Wenn es keine reellen Lösungen gibt, schneidet der Strahl die Kugel nicht. Gibt es genau eine Lösung, dann berührt der Strahl die Kugel. Andernfalls geben die beiden Lösungen die Schnittpunkte mit der Kugel an. Der Schnittpunkt mit dem kleinsten positiven $t$-Wert liegt am nächsten.

Man muß zur Schattierung der Fläche die Flächennormale im Schnittpunkt berechnen. Im Fall der Kugel ist das besonders einfach, weil die (nicht normalisierte) Normale einfach der Vektor vom Kugelmittelpunkt zum Schnittpunkt ist: Die Kugel mit Mittelpunkt $(a, b, c)$ hat im Schnittpunkt $(x,y,z)$ die Flächennormale $((x-a)/r, (y-b)/r, (z-c)/r)$.

Es ist etwas schwieriger, den Schnittpunkt des Strahls mit einem Polygon zu berechnen. Um festzustellen, ob der Strahl ein Polygon schneidet, testet man zuerst, ob der Strahl die Ebene des Polygons schneidet und anschließend, ob der Schnittpunkt innerhalb des Polygons liegt.