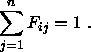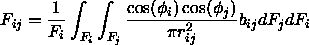
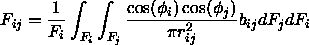
mit
| Winkel zwischen Normale auf Fläche |
||
| Winkel zwischen Normale auf Fläche |
||
| Entfernung zwischen Fläche |
||
| Blockierungsfunktion, falls Teile von Fläche |
||
| Flächeninhalt von Fläche |
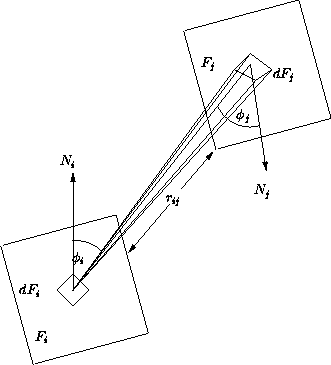
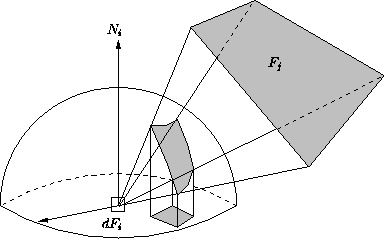
Die geometrische Interpretation beschreibt den Formfaktor
als das Verhältnis der Basisfläche einer Halbkugel
zur Orthogonalprojektion der auf die Halbkugel projizierten
Fläche:
Erst projiziert man die von ![]() aus sichtbaren Teile von
aus sichtbaren Teile von
![]() auf eine Halbkugel mit Radius Eins um
auf eine Halbkugel mit Radius Eins um
![]() , projiziert diese Projektion orthogonal auf die
kreisförmige Grundfläche der Halbkugel und dividiert schließlich
durch die Kreisfläche.
Die Projektion auf die halbe Einheitskugel entspricht in der
Gleichung dem Term
, projiziert diese Projektion orthogonal auf die
kreisförmige Grundfläche der Halbkugel und dividiert schließlich
durch die Kreisfläche.
Die Projektion auf die halbe Einheitskugel entspricht in der
Gleichung dem Term
![]() , die Projektion auf die
Grundfläche entspricht der Multiplikation mit
, die Projektion auf die
Grundfläche entspricht der Multiplikation mit ![]() ,
und die Division durch den Flächeninhalt des Einheitskreises
liefert den Wert
,
und die Division durch den Flächeninhalt des Einheitskreises
liefert den Wert ![]() im Nenner.
im Nenner.
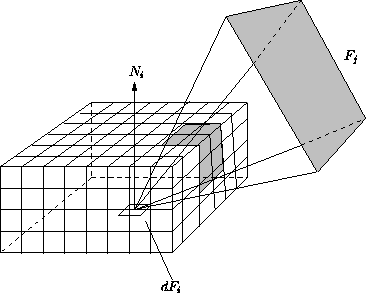
Zur numerischen Berechnung wird die Halbkugel
durch einen
Halbwürfel
(hemi-cube) mit dem Zentrum
im Ursprung und dem Normalvektor in der ![]() -Achse
ersetzt.
Die Oberseite des Würfels ist dabei parallel zur Fläche.
Jede Seite des Halbwürfels wird in ein Raster gleich
großer quadratischer Zellen aufgeteilt.
(Die Auflösungen reichen von
-Achse
ersetzt.
Die Oberseite des Würfels ist dabei parallel zur Fläche.
Jede Seite des Halbwürfels wird in ein Raster gleich
großer quadratischer Zellen aufgeteilt.
(Die Auflösungen reichen von ![]() bis zu mehreren Hundert
pro Seite.)
Dann wird jedes Flächenelement auf die
Seiten des Halbwürfels projiziert.
Dazu benutzt man einen Algorithmus, der für jede Zeile die Kennung
des nächsten schneidenden Elements speichert.
Diese Elementpuffer kann man mit einem
bis zu mehreren Hundert
pro Seite.)
Dann wird jedes Flächenelement auf die
Seiten des Halbwürfels projiziert.
Dazu benutzt man einen Algorithmus, der für jede Zeile die Kennung
des nächsten schneidenden Elements speichert.
Diese Elementpuffer kann man mit einem ![]() -Puffer-Algorithmus für
jede Seite des Halbwürfels berechnen, bei dem man für jede Zelle
statt der Schattierung die Kennung der nächstliegenden Fläche speichert.
Jeder Zelle des Halbwürfels ist ein Delta-Formfaktor zugeordnet,
der von der Position der Zelle abhängt und vorher berechnet wird.
Für eine beliebig feine Rasterung der Quaderoberfläche
ergibt sich der Formfaktor
-Puffer-Algorithmus für
jede Seite des Halbwürfels berechnen, bei dem man für jede Zelle
statt der Schattierung die Kennung der nächstliegenden Fläche speichert.
Jeder Zelle des Halbwürfels ist ein Delta-Formfaktor zugeordnet,
der von der Position der Zelle abhängt und vorher berechnet wird.
Für eine beliebig feine Rasterung der Quaderoberfläche
ergibt sich der Formfaktor ![]() als Summe
aller von der Fläche
als Summe
aller von der Fläche ![]() überdeckten Rasterzellen.
Wird eine Rasterzelle von mehreren Flächen
überdeckt, wird sie der Fläche mit der geringsten
Entfernung zugerechnet.
Für die Summe aller
Formfaktoren einer Fläche
überdeckten Rasterzellen.
Wird eine Rasterzelle von mehreren Flächen
überdeckt, wird sie der Fläche mit der geringsten
Entfernung zugerechnet.
Für die Summe aller
Formfaktoren einer Fläche ![]() gilt
gilt