8.3 Fraktale Dimension

Ein selbstähnliches Objekt hat Dimension D , falls es in N identische Kopien unterteilt werden kann, die jeweils skaliert sind mit dem Faktor r=.

Beispiel:

Linie hat Dimension 1 , denn sie besteht aus N Stücken der Größe .
Quadratische Fläche hat Dimension 2 , denn sie besteht aus N Flächen der Größe ,
z.B. 9 Teilflächen mit Kantenlängen skaliert um r==

Sind N und r bekannt, läßt sich D bestimmen:

Beispiel:

Die Koch'sche Schneeflocke hat Dimension D = = 1.2618 , denn jeder Kantenzug besteht aus N = 4 Kopien, jeweils skaliert um den Faktor r = .

/*****************************************************************************/
/*                                                                           */
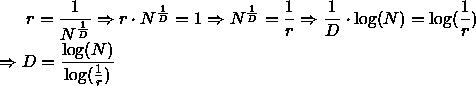
/*                        Koch'sche Schneeflocke                             */
/*                                                                           */
/*****************************************************************************/

private int koch_stern(         // wendet eine Koch-Iteration an auf
        Point poly_punkt[],     // das Polygon poly_punkt
        int poly_punkt_cnt)     // mit poly_point_cnt Punkten
                                // neue Anzahl Punkte wird zurueckgeliefert
{
        int i,j;
        double x0,x1,x2,x3,x4,y0,y1,y2,y3,y4;
        Point[] HPunkt = new Point[MAX_POINTS];
        j=0;

        for (i=0; i < poly_point_cnt; i++)
        {
                x0 = poly_punkt[i].x;
                y0 = poly_punkt[i].y;
                
                x4 = poly_punkt[(i+1)%(poly_point_cnt)].x;
                y4 = poly_punkt[(i+1)%(poly_point_cnt)].y;

                x1 = (x4-x0)/3+x0;
                y1 = (y4-y0)/3+y0;
                        
                x3 = x4 - (x4-x0)/3;
                y3 = y4 - (y4-y0)/3;

                x2 = (int)(x1+ (x3-x1)*cos_60 - (y3-y1)*sin_60);
                y2 = (int)(y1+ (y3-y1)*cos_60 + (x3-x1)*sin_60);

                HPunkt[j]   = new Point();
                HPunkt[j+1]   = new Point();
                HPunkt[j+2]   = new Point();
                HPunkt[j+3]   = new Point();

                HPunkt[j]        = poly_punkt[i];
                HPunkt[j+1].x        = (int)x1;
                HPunkt[j+1].y        = (int)y1;
                HPunkt[j+2].x        = (int)x2;
                HPunkt[j+2].y        = (int)y2;
                HPunkt[j+3].x        = (int)x3;
                HPunkt[j+3].y        = (int)y3;
                j=j+4;
        }

        for (i=0; i < j; i++)                // neu berechnetes Polygon 
                poly_punkt[i] = HPunkt[i];   // kopieren

        return j;                            // neue Anzahl Punkte zurueck
}