Der hier vorgestellte z-Buffer-Algorithmus löst das Problem nach dem folgenden Prinzip: Für alle Pixel des Bildschirms wird die z -Komponente als Wert für die Tiefe im Raum gespeichert. Die benötigte Datenstruktur, der sogenannte z-Buffer, ist im Programm ein 2-dimensionales Array, das für jedes Pixel den z -Wert des in diesem Punkt dem Betrachter am nächsten liegenden Objekts enthält. In einem gleichgroßen Feld, dem Frame Buffer, werden die Farbwerte der Pixel gespeichert. Die Menge der Farbwerte stellt den Bildschirmspeicher dar.
Der z -Wert wird mit Null und der Farbwert mit der Hintergrundfarbe der Szene initialisiert.
Laut Definition der Transformationspipeline treten nach dem Clipping im NPC nur noch z -Werte zwischen Null und Eins auf. Die Initialisierung mit Null entspricht dem größtmöglichen Abstand vom Betrachter (back plane).
Durch die Rasterung der Flächen erhalten die Pixel auch einen interpolierten z -Wert, der mit dem z-Buffer-Wert an dieser Stelle verglichen wird. Ist der z -Wert des Pixels größer, so ist das Pixel (vorläufig) sichtbar. Sein z -Wert wird in den z-Buffer und sein Farbwert in den Bildschirmspeicher eingetragen. Ist der z -Wert des Pixels kleiner, so ist der zugehörige Teil der Fläche verdeckt; die Inhalte von z-Buffer und Bildschirmspeicher bleiben erhalten. Nach der Abarbeitung aller Flächen enthält der Bildschirmspeicher die Abbildung der sichtbaren Flächen bzw. Flächenteile und der z-Buffer die zugehörige Tiefeninformation.
Der z-Buffer-Algorithmus entscheidet pixelweise über die Verdeckungseigenschaften und ist daher sehr allgemeingültig. Die darzustellenden ebenen Flächen brauchen nicht vorsortiert zu werden und dürfen sich gegenseitig durchdringen. Da er am Ende der Transformationspipeline im DC arbeitet, wird er als Bildraumalgorithmus klassifiziert.
Der z-Buffer-Algorithmus wird vom Programm in der inneren Schleife des Scanline-Algorithmus aufgerufen und läßt sich wie folgt skizzieren:
Für jede Fläche F tue:
Für jedes Pixel (x, y) auf dieser Fläche tue:
berechne Farbe c und Tiefe z
falls z > tiefe[x, y]:
dann wird c an der Stelle x,y im Frame Buffer eingetragen
und tiefe[x, y] auf z gesetzt.
Ist die Fläche durch
Ax + By + Cz + D = 0 gegeben, so ist die Tiefe im Punkt
(x,y) :
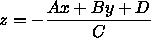
Für auf einer Scanline benachbarte Punkte
(xi,yj) und
(xi + 1,yj) ergibt sich
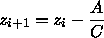
Für die Punkte
(xi,yj) und
(xi,yj + 1) zweier
benachbarter Scanlines ergibt sich
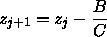
Das größte Problem bei der Implementierung des z-Buffers ist sein Speicherplatzbedarf. Eine ausreichende Auflösung der Tiefeninformation ergibt sich erst mit einem 32-Bit z -Wert, d.h. maxint = (231 - 1) . Für die RGB-Tripel werden drei Byte benötigt, die in einem 32-Bit Integer kodiert werden. Pro Pixel belegen der z-Buffer und der Bildschirmspeicher also acht Byte. Bei einer Bildschirmauflösung von 1024 × 768 Pixeln ergeben sich folglich 6 MB.