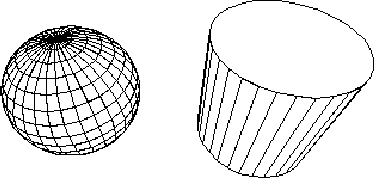
Die Oberfläche einer Kugel mit Radius 1 kann beschrieben
werden durch
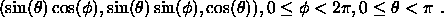
Zur Approximation durch Flächen wird der Vollwinkel in
n Teile zerlegt:
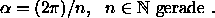
Dadurch entstehen auf der Kugel n/2 gleichgroße Längenkreise und (n/2 - 1)
verschieden große Breitenkreise.
Diese schneiden n Dreiecke an jedem Pol und
n(n/2 - 2) Vierecke aus
der Kugeloberfläche.
Die Ortsvektoren der Eckpunkte eines Dreiecks am Nordpol
(![]() = 0) lauten
= 0) lauten
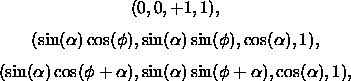
mit
![]() = k ·
= k · ![]() ,
k
,
k ![]() {0,...,n - 1} .
{0,...,n - 1} .
Die Eckpunkte eines der Vierecke haben die Ortsvektoren
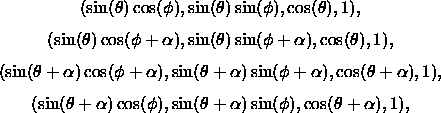
mit
![]() = k ·
= k · ![]() ,k
,k ![]()
![]() ,k < n und
,k < n und
![]() = l ·
= l · ![]() ,l
,l ![]()
![]() ,0 < l < (n/2 - 1) .
,0 < l < (n/2 - 1) .
Als Normalenvektor wird in jedem Eckpunkt der Ortsvektor als Richtungsvektor ( w = 0 ) eingetragen, denn der Radiusvektor steht senkrecht auf der Kugeloberfläche. Einen Ellipsoid erzeugt der Rendering-Algorithmus aus der Kugel durch ungleichmäßige Skalierung beim Modeling.
Abbildung 16.3 zeigt eine vom Projektionsalgorithmus erzeugte Szene mit Kugel und Zylinder in der Drahtmodell-Darstellung ohne Rückkanten ( n = 32 ).